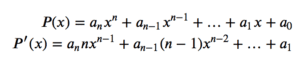튜토리얼 개요

이 자습서는 다음과 같이 두 부분으로 나뉩니다.

1. x의 정수 거듭제곱을 포함하는 함수의 도함수
2. x의 0이 아닌 실제 거듭제곱을 갖는 함수의 미분

두 함수의 합 도함수

두 함수의 합을 제어하는 간단한 규칙을 찾는 것으로 시작하겠습니다. 두 개의 함수 f(x)와 g(x)가 있다고 가정하면 합계의 도함수는 다음과 같이 찾을 수 있습니다. 검토가 필요한 경우 파생 상품의 정의를 참조 할 수 있습니다.

두 함수의 합 도함수

여기에는 두 함수의 합 도함수의 도함수가 개별 함수의 도함수의 합이라는 일반적인 규칙이 있습니다.

x의 정수 거듭제곱의 도함수

x의 정수 거듭제곱의 도함수에 대해 이야기하기 전에 다음 표현식을 확장하는 방법을 알려주는 이항 정리를 검토해 보겠습니다(여기서 C(n,k)는 선택 함수임).

(a+b)^n = a^n + C(n,1)a^(n-1)b + C(n,2)a^(n-2)b^2 + … + C(n,n-1)ab^(n-1) + b^n

x^n을 포함하는 함수의 도함수를 찾기 위한 간단한 규칙을 도출할 것이며, 여기서 n은 정수이고 n>0입니다. 이 튜토리얼에서 설명한 도함수의 정의로 돌아가서 kx^n에 적용해 보겠습니다. 여기서 k는 상수입니다.

kx^n의 도함수

다음은 이 규칙을 적용하는 몇 가지 예입니다.

• x^2의 도함수는 2x입니다.
• 3x^5의 도함수는 15x^4입니다.
• 4x^9의 도함수는 36x^8입니다.

다항식을 미분하는 방법?

두 규칙, 즉 두 함수의 합 도함수에 대한 규칙과 x의 정수 거듭제곱의 도함수에 대한 규칙을 통해 다항식을 미분할 수 있습니다. 차수가 n인 다항식이 있는 경우 x의 다른 거듭제곱을 포함하는 개별 함수의 합으로 간주할 수 있습니다. 차수가 n인 다항식 P(x)가 있다고 가정하면 그 도함수는 P'(x)로 다음과 같이 주어집니다.

다항식의 도함수

이것은 차수 n의 다항식의 도함수가 실제로 차수 (n-1)의 다항식임을 보여줍니다.

예제

다항식 함수와 그 도함수가 모두 함께 그려지는 몇 가지 예가 아래에 나와 있습니다. 파란색 곡선은 함수 자체를 나타내고 빨간색 곡선은 해당 함수의 도함수입니다.

다항식 함수와 그 도함수의 예

x의 정수가 아닌 거듭제곱은 어떻습니까?

위에서 파생 된 규칙은 x의 정수가 아닌 실수의 거듭 제곱으로 확장되며, 이는 분수, 음수 또는 무리수 일 수 있습니다. 일반적인 규칙은 아래에 나와 있으며, 여기서 a와 k는 0이 아닌 실수가 될 수 있습니다.

f(x) = kx^a

f'(x) = kax^(a-1)

몇 가지 예는 다음과 같습니다.

• x^(0.2)의 도함수는 (0.2)x^(-0.8)입니다.
• x^(π)의 도함수는 πx^(π-1)입니다.
• x^(-3/4)의 도함수는 (-3/4)x^(-7/4)입니다.

다음은 파생 상품과 함께 플롯 된 몇 가지 예입니다. 다시 말하지만, 파란색 곡선은 함수 자체를 나타내고 빨간색 곡선은 해당 도함수를 나타냅니다.

x의 실수 거듭제곱을 포함하는 표현식의 도함수의 예

확장

이 섹션에는 탐색할 수 있는 자습서를 확장하기 위한 몇 가지 아이디어가 나열되어 있습니다.

• 두 함수의 곱의 도함수에 대한 규칙
• 합리적인 함수의 도함수에 대한 규칙
• 통합

추가 정보¶

이 섹션에서는 더 자세히 알아보려는 경우 주제에 대한 더 많은 리소스를 제공합니다.

자습서

• 한계와 연속성
• 한계 평가
• 파생 상품

리소스¶

• 머신러닝을 위한 미적분학 책에 대한 추가 리소스

책

• 토마스의 미적분학, 14판, 2017. (조지 B. 토마스의 원작을 바탕으로 조엘 하스, 크리스토퍼 하일, 모리스 위어 수정)
• 미적분학, 제 3 판, 2017. (길버트 스트랭)
• 미적분학, 8판, 2015. (제임스 스튜어트)

요약

이 자습서에서는 다항식 함수와 x의 정수가 아닌 거듭제곱의 합을 포함하는 함수를 구별하는 방법을 알아보았습니다.

특히 다음 내용을 배웠습니다.

• 두 함수의 합 도함수
• 상수에 x의 정수 거듭제곱을 곱한 미분
• 다항식 함수의 도함수
• x의 정수가 아닌 거듭제곱을 포함하는 표현식의 합 도함수