튜토리얼 개요

이 자습서는 다음과 같이 두 부분으로 나뉩니다. 

1. 최적화와 관련된 다양한 입문 주제
   1. 제약 조건 최적화 vs. 제약 조건 없는 최적화
   2. 평등 vs. 불평등 제약 조건
   3. 실현 가능한 지역
2. 머신러닝의 최적화 예

최적화 또는 수학적 프로그래밍이란 무엇입니까?

미적분학과 수학에서 최적화 문제는 수학적 프로그래밍이라고도 합니다. 이 문제를 간단히 설명하기 위해 주어진 기준 또는 제약 조건에 가장 적합한 요소, 변수 또는 수량을 찾을 수 있는 메커니즘입니다.

최대화 대 최소화 문제

최적화 문제의 가장 간단한 경우는 스칼라 함수의 최소화 또는 최대화입니다. 하나 이상의 변수로 구성된 스칼라 함수가 있는 경우 f(x_1, x_2, … x_n) 다음은 최적화 문제입니다.

f(x)가 최소값인 x_1, x_2, …, x_n 찾기

또는 동등한 최대화 문제가 있을 수 있습니다.

오류 또는 페널티를 정량화하는 함수를 정의할 때 최소화 문제를 적용합니다. 반면에 학습 알고리즘이 메서드의 정확도를 모델링하는 함수를 구성하면 이 함수를 최대화할 수 있습니다.

최적화를 위한 많은 자동화된 소프트웨어 도구는 일반적으로 최대화 문제 또는 최소화 작업을 구현하지만 둘 다 구현하지는 않습니다. 따라서 f(x)에 음수 부호를 추가하여 최대화 문제를 최소화 문제로(또는 그 반대로) 변환할 수 있습니다. 

최대화 f(x) w.r.r x는 최소화 -f(x) wrt x와 같습니다.

두 문제가 동일하므로 자습서의 나머지 부분에서는 최소화 또는 최대화 문제에 대해서만 이야기하겠습니다. 동일한 규칙과 정의가 동등한 것에 적용됩니다.

글로벌 vs. 로컬 최적 포인트

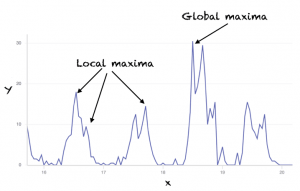
머신러닝에서 우리는 종종 복잡한 환경에서 매우 비선형적인 함수를 접하게 됩니다. 함수가 해당 지점 주변의 작은 영역 또는 로컬 영역 내에서 가장 낮은 값을 갖는 지점이 있을 수 있습니다. 이러한 점을 로컬 최소점이라고합니다.

이는 함수가 전체 도메인에서 가장 작은 값을 갖는 지점인 전역 최소값과 반대됩니다. 다음 그림에서는 로컬 및 전역 최대 지점을 보여 줍니다.

지역 및 글로벌 최대 포인트

제약 조건이 없는 최적화 vs. 제약 조건이 있는 최적화

머신러닝에는 많은 문제가 있으며, 제약이나 제한없이 글로벌 최적 지점을 찾는 데 관심이 있습니다. 이러한 문제를 제약 조건이 없는 최적화 문제라고 합니다.

때때로 우리는 특정 제약 조건에 따라 최적화 문제를 해결해야 합니다. 이러한 최적화 문제를 제약 조건이 있는 최적화 문제라고 합니다. 예를 들어:

x + y <= 1일 경우 x^2 + y^2을 최소화합니다.  

제약 조건 최적화의 예는 다음과 같습니다.

1. 도메인의 변수 합이 1이어야 하는 경우 함수의 최소값 찾기
2. 특정 벡터가 서로 수직이되도록 함수의 최소값 찾기
3. 특정 도메인 변수가 특정 범위에 있도록 함수의 최소값을 찾습니다.

실현 가능한 지역

문제에 대한 제약 조건이 참인 공간의 모든 점은 실현 가능한 영역을 구성합니다. 최적화 알고리즘은 실현 가능한 영역에서 최적의 지점을 검색합니다. 두 가지 유형의 제약 조건에 대해 실행 가능한 영역은 다음 섹션의 그림에 나와 있습니다.

제약 조건이 없는 최적화 문제의 경우 함수의 전체 도메인이 실행 가능한 영역입니다.

평등 대 불평등 제약 조건

최적화 문제에 부과된 제약 조건은 같음 제약 조건 또는 같지 제약 조건일 수 있습니다. 아래 그림에서는 두 가지 유형의 제약 조건을 보여 줍니다.

평등 vs. 불평등 제약 조건

선형 대 비선형 계획법

함수가 선형이고 모든 같음 또는 부등식 제약 조건도 선형 제약 조건인 최적화 문제를 선형 프로그래밍 문제라고 합니다.

목적 함수가 비선형이거나 하나 이상의 제약 조건이 비선형이면 비선형 프로그래밍 문제가 발생합니다.

선형 함수와 비선형 함수의 차이를 시각화하려면 아래 그림을 확인하십시오.

선형 함수 vs. 비선형 함수

머신러닝의 최적화 예

다음은 최적화를 사용하는 잘 알려진 머신러닝 알고리즘입니다. 거의 모든 머신러닝 알고리즘은 일종의 최적화를 사용한다는 점을 명심해야 합니다.

1. 신경망의 경사하강법(제약 없는 최적화).
2. 서포트 벡터 머신에서 라그랑주 승수의 방법(제약 조건 최적화).
3. 주성분 분석(제약 조건 최적화) 
4. 기대 최대화 알고리즘을 통한 클러스터링(제한된 최적화)
5. 로지스틱 회귀(제약 조건이 없는 최적화)
6. 진화 학습 알고리즘의 유전 알고리즘 (제약 및 제약 조건이 없는 최적화 문제를 모두 해결하기 위해 다양한 변형이 존재함).

확장

이 섹션에는 탐색할 수 있는 자습서를 확장하기 위한 몇 가지 아이디어가 나열되어 있습니다.

• 라그랑주 승수의 방법
• 비선형 최적화 기술
• 심플렉스 방법

추가 정보

이 섹션에서는 더 자세히 알아보려는 경우 주제에 대한 더 많은 리소스를 제공합니다.

자습서

• 여러 변수와 기울기 벡터의 함수
• 머신러닝을 위한 경사하강법
• 머신러닝에서 최적화가 중요한 이유
• 최적화 알고리즘을 선택하는 방법

리소스

• 머신러닝을 위한 미적분학 책에 대한 추가 리소스

책

• 토마스의 미적분학, 14판, 2017. (조지 B. 토마스의 원작을 바탕으로 조엘 하스, 크리스토퍼 하일, 모리스 위어 수정)
• 미적분학, 제 3 판, 2017. (길버트 스트랭)
• 미적분학, 8판, 2015. (제임스 스튜어트)

요약

이 튜토리얼에서는 수학적 프로그래밍 또는 최적화 문제가 무엇인지 발견했습니다. 특히 다음 내용을 배웠습니다.

• 최대화 vs. 최소화
• 제약 조건 최적화 vs. 제약 조건 없는 최적화
• 머신러닝에서 최적화가 중요한 이유