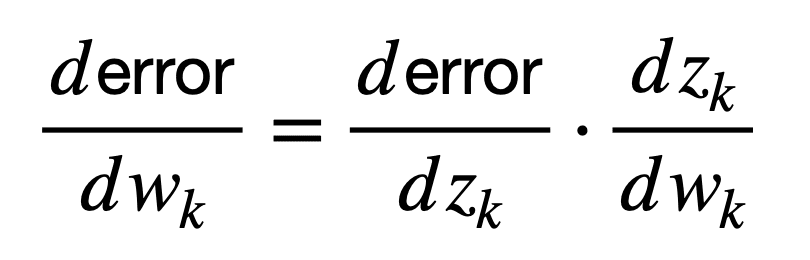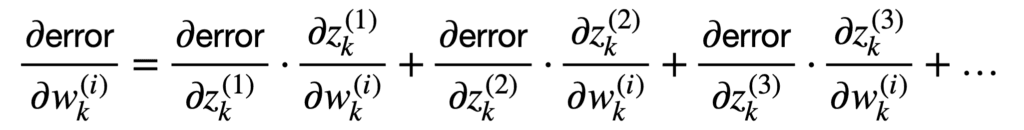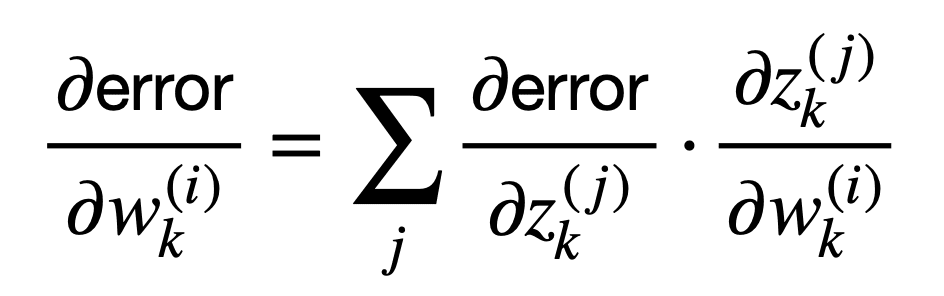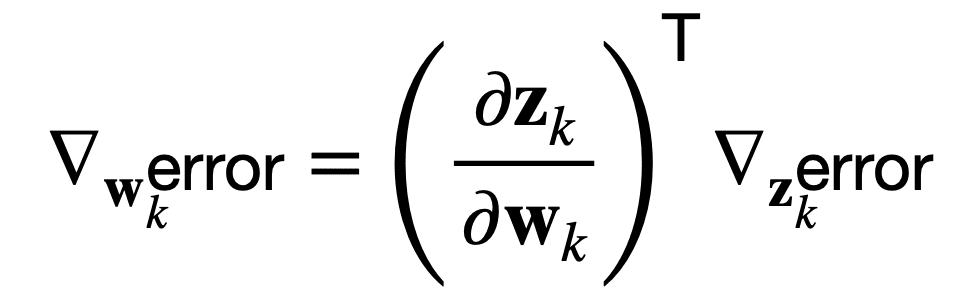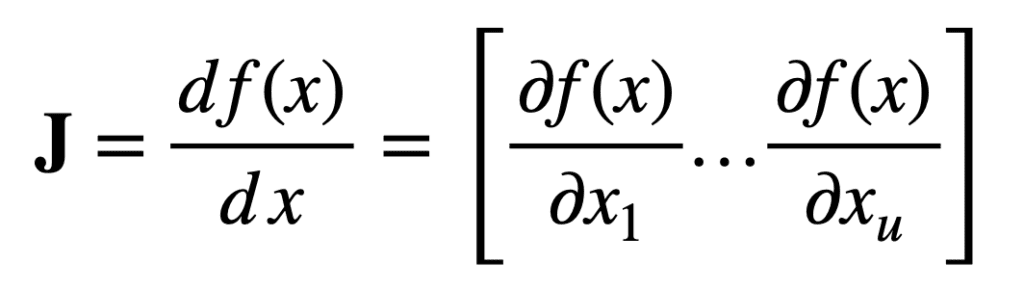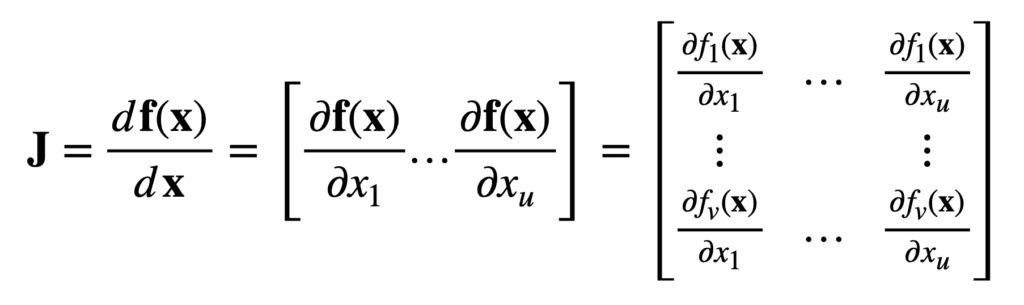튜토리얼 개요

이 자습서는 다음과 같이 세 부분으로 나뉩니다.

• 머신러닝의 부분 파생 상품
• 야코비 행렬
• 야코비안의 다른 용도

머신러닝의 부분 파생 상품

지금까지 그래디언트와 편미분은 최적화 알고리즘이 신경망의 모델 가중치를 업데이트하여 최적의 가중치 집합에 도달하는 데 중요하다고 언급했습니다. 편미분을 사용하면 각 가중치에 대한 오차 곡선의 기울기를 차례로 계산하여 각 가중치를 다른 가중치와 독립적으로 업데이트 할 수 있습니다.

머신러닝에서 일반적으로 작업하는 많은 함수는 다변량의 벡터 값 함수이며, 이는 여러 개의 실제 입력 n을 여러 개의 실제 출력 m에 매핑한다는 것을 의미합니다.

예를 들어, 회색조 영상을 여러 클래스로 분류하는 신경망을 생각해 보십시오. 이러한 분류자에 의해 구현되는 함수는 각각의 단일 채널 입력 이미지의 n 픽셀 값을 각각의 상이한 클래스에 속하는 m 개의 출력 확률에 매핑합니다. 

신경망을 훈련시킬 때, 역전파 알고리즘은 입력값에 도달할 때까지 신경망의 서로 다른 숨겨진 계층을 구성하는 뉴런 간에 출력 계층에서 계산된 오류를 다시 공유하는 역할을 합니다. 

네트워크에서 가중치를 조정할 때 역전파 알고리즘의 기본 원칙은 네트워크의 각 가중치가 해당 가중치의 변화에 대한 네트워크의 전체 오차 민감도에 비례하여 업데이트되어야 한다는 것입니다.

– 페이지 222, 딥 러닝, 2019.

임의의 특정 가중치의 변화에 대한 네트워크의 전체 오차의 민감도는 변화율의 관점에서 측정되며, 이는 차례로 동일한 가중치에 대한 오차의 부분 도함수를 취하여 계산됩니다. 

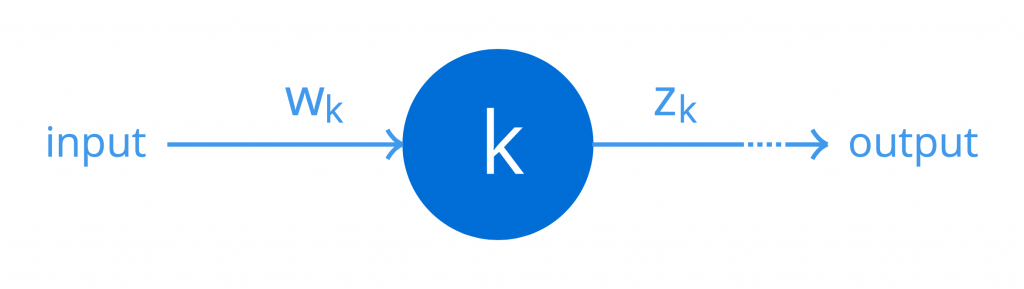
간단히 하기 위해, 특정 네트워크의 숨겨진 계층 중 하나가 단 하나의 뉴런 k로 구성되어 있다고 가정해 보겠습니다. 우리는 이것을 간단한 계산 그래프의 관점에서 나타낼 수 있습니다.

단일 입력과 단일 출력을 갖는 뉴런

다시 말하지만, 단순화를 위해 가중치, wk, 이 뉴런의 입력에 적용되어 출력을 생성하고, zk,이 뉴런이 구현하는 기능 (비선형 성 포함)에 따릅니다. 그런 다음 이 뉴런의 가중치를 다음과 같이 네트워크 출력값의 오류에 연결할 수 있습니다(다음 공식은 공식적으로 미적분학의 연쇄 규칙으로 알려져 있지만 나중에 별도의 자습서에서 자세히 설명합니다).

여기서, 도함수는, dzk / DWk, 먼저 무게를 연결하고, wk, 출력으로, zk, 도함수 동안, d오차/dzk, 이어서 출력을 zk, 네트워크 오류로 연결합니다.

네트워크를 채우는 많은 연결된 뉴런이 각각 다른 가중치를 부여하는 경우가 더 많습니다. 이러한 시나리오에 더 관심이 있기 때문에 스칼라 사례를 넘어 일반화하여 여러 입력과 여러 출력을 고려할 수 있습니다.

이 용어의 합은 다음과 같이 더 간결하게 나타낼 수 있습니다.

또는 동등하게, del 연산자 ∇를 사용하는 벡터 표기법에서 가중치 w k또는 출력값, zk:

역전파 알고리즘은 그래프의 각 연산에 대해 이러한 야코비 기울기 곱을 수행하는 것으로 구성됩니다.

– 페이지 207, 딥 러닝, 2017.

이는 역전파 알고리즘이 야코비 행렬(∂z)에 의한 곱셈을 통해 네트워크 오류의 민감도를 가중치의 변화와 관련시킬 수 있음을 의미합니다.k / ∂여k)T.

따라서 이 야코비 행렬에는 무엇이 포함되어 있습니까?

야코비 행렬

야코비 행렬은 다변량 함수의 모든 1차 편도함수를 수집합니다.

특히, 먼저 u 실수 입력을 단일 실수 출력에 매핑하는 함수를 고려하십시오.

그런 다음 길이가 u인 입력 벡터 x에 대해 크기가 1 × u인 야코비 행렬 벡터를 다음과 같이 정의할 수 있습니다.

이제 u 실수 입력을 v 실수 출력에 매핑하는 또 다른 함수를 고려하십시오.

그런 다음 길이가 u인 동일한 입력 벡터 x에 대해 야코비 행렬은 이제 v × u 행렬 J ∈ R 이 됩니다.v×u, 다음과 같이 정의됩니다.

야코비 행렬을 앞에서 고려한 머신러닝 문제로 재구성하면서 동일한 수의 u 실수 입력값과 v 실수 출력을 유지하면서 이 행렬에 다음과 같은 편미분이 포함된다는 것을 알 수 있습니다.

야코비안의 다른 용도

적분으로 작업할 때 중요한 기술은 적분이 계산하기 쉬운 다른 적분으로 단순화되는 변수 변경 (치환 또는 u- 치환에 의한 적분이라고도 함)을 포함합니다. 

단일 변수의 경우 일부 변수 x를 다른 변수 u로 대체하면 원래 함수를 역미분을 더 쉽게 찾을 수 있는 더 간단한 함수로 변환할 수 있습니다. 두 변수의 경우, 또 다른 이유는 우리가 통합하려는 항의 영역을 다른 모양으로 변환하기를 원할 수도 있습니다. 

단일 변수의 경우 일반적으로 변수를 변경하려는 한 가지 이유가 있습니다 : 역파생 함수를 찾을 수 있도록 함수를 “더 멋지게” 만드는 것입니다. 두 변수의 경우, 두 번째 잠재적인 이유가 있습니다 : 우리가 통합해야 하는 2 차원 영역은 다소 불쾌하며, 우리는 u와 v의 관점에서 영역이 더 좋기를 원합니다 (예 : 직사각형).

– 페이지 412, 단일 및 다변수 미적분학, 2020.

두 개(또는 그 이상)의 변수 사이에서 대체를 수행할 때 프로세스는 대체가 발생할 변수의 정의로 시작합니다. 예를 들어 x = f(u, v) 및 y = g(u, v)입니다. 그런 다음 함수 f 및 g가 u–v 평면을 x–y 평면으로 변환하는 방법에 따라 적분 한계를 변환합니다. 마지막으로, 야코비 행렬식의 절대값이 계산되고 포함되어 한 좌표 공간과 다른 좌표 공간 사이의 배율 인수로 작동합니다. 

추가 정보

이 섹션에서는 더 자세히 알아보려는 경우 주제에 대한 더 많은 리소스를 제공합니다.

책

• 딥 러닝, 2017.
• 머신러닝을 위한 수학, 2020.
• 단일 및 다변수 미적분학, 2020.
• 딥 러닝, 2019.

기사

• 야코비 행렬과 행렬식, 위키피디아.
• 대체에 의한 통합, 위키백과.

요약

이 튜토리얼에서는 Jacobian에 대한 다음 내용을 배웠습니다.

• 야코비 행렬은 역전파에 사용할 수 있는 다변량 함수의 모든 1차 편도함수를 수집합니다.
• 야코비 행렬식은 한 좌표 공간과 다른 좌표 공간 사이의 배율 인자 역할을 하는 변수 사이를 변경하는 데 유용합니다.