파이썬에서 Basin hopping 최적화

16 12월

파이썬에서 Basin hopping 최적화

by Nepirity

in Technology

Comments

Basin hopping은 전역 최적화 알고리즘입니다.

화학 물리학의 문제를 해결하기 위해 개발되었지만 다중 최적을 가진 비선형 목적 함수에 적합한 효과적인 알고리즘입니다.

이 튜토리얼에서는 Basin hopping 전역 최적화 알고리즘을 발견하게 됩니다.

이 자습서를 완료하면 다음을 알 수 있습니다.

Basin hopping 최적화는 무작위 섭동을 사용하여 basin을 점프하고 로컬 검색 알고리즘을 사용하여 각 basin을 최적화하는 글로벌 최적화입니다.
파이썬에서 Basin hopping 최적화 알고리즘 API를 사용하는 방법.
Basin hopping을 사용하여 다중 최적으로 글로벌 최적화 문제를 해결하는 예제.

튜토리얼 개요

이 자습서는 다음과 같이 세 부분으로 나뉩니다.

Basin hopping 최적화
Basin hopping API
Basin hopping 예제
1. 로컬 옵티마를 사용한 다중 모드 최적화
2. 다중 글로벌 최적을 사용한 다중 모드 최적화

Basin hopping 최적화

Basin Hopping은 화학 물리학 분야에서 사용하기 위해 개발된 글로벌 최적화 알고리즘입니다.

Basin hopping (BH) 또는 몬테카를로 최소화 (MCM)는 지금까지 원자 클러스터 및 거대 분자 시스템의 가장 낮은 에너지 구조를 검색하기위한 화학 물리학에서 가장 신뢰할 수있는 알고리즘입니다.

— 가끔 점프하는 Basin hopping, 2004.

로컬 최적화는 일변량 목적 함수에 대한 최적값을 찾거나 최적값이 존재한다고 생각되는 영역에서 작동하기 위한 최적화 알고리즘을 나타냅니다. 전역 최적화 알고리즘은 잠재적으로 여러 로컬 (비 전역) 최적 중에서 단일 전역 최적을 찾기위한 것입니다.

Basin hopping은 데이비드 웨일즈 (David Wales)와 조나단 도이 (Jonathan Doye)가 1997 년 논문 “Basin hopping에 의한 글로벌 최적화와 최대 110 개의 원자를 포함하는 레나드 존스 클러스터의 최저 에너지 구조“라는 제목의 논문에서 설명했습니다.

알고리즘에는 좋은 후보 솔루션의 섭동과 교란된 솔루션에 대한 로컬 검색의 적용이라는 두 단계를 순환하는 작업이 포함됩니다.

[Basin hopping]은 복잡한 에너지 풍경을 분지의 집합으로 변환하고 메트로폴리스 기준을 사용하여 임의의 몬테카를로 이동 및 수락/거부에 의해 달성되는 호핑을 통해 탐색합니다.

— 가끔 점프하는 Basin hopping, 2004.

섭동은 검색 알고리즘이 검색 공간의 새로운 영역으로 점프하고 잠재적으로 다른 최적으로 이어지는 새로운 분지를 찾을 수있게합니다 (예 : 기술 이름의 “Basin hopping“).

로컬 검색을 통해 알고리즘은 새 basin을 최적으로 횡단할 수 있습니다.

새로운 최적은 새로운 무작위 섭동의 기초로 유지 될 수 있으며, 그렇지 않으면 폐기됩니다. 새 솔루션을 유지하기로 한 결정은 시뮬레이션된 어닐링과 마찬가지로 “온도” 변수가 있는 확률적 결정 함수에 의해 제어됩니다.

온도는 알고리즘의 반복 횟수의 함수로 조정됩니다. 이를 통해 온도가 높을 때 실행 초기에 임의의 솔루션을 수락 할 수 있으며 나중에 온도가 낮을 때 검색에서 더 나은 품질의 솔루션 만 수락하는보다 엄격한 정책을 사용할 수 있습니다.

이러한 방식으로 알고리즘은 서로 다른 (교란된) 시작점을 가진 반복된 로컬 검색과 매우 유사합니다.

알고리즘은 지정된 반복 횟수 또는 함수 평가에 대해 실행되며 여러 번 실행하여 전역 최적값을 찾았는지 또는 상대적으로 양호한 솔루션을 찾았는지에 대한 신뢰도를 높일 수 있습니다.

이제 높은 수준의 기본 호핑 알고리즘에 익숙해졌으므로 Python에서 Basin hopping을 위한 API를 살펴보겠습니다.

Basin hopping API

Basin hopping은 파이썬에서 basinhopping() SciPy 함수를 통해 사용할 수 있습니다.

이 함수는 최소화할 목적 함수의 이름과 초기 시작점을 사용합니다.

1
2
3
...
# perform the basin hopping search
result = basinhopping(objective, pt)

또 다른 중요한 하이퍼 매개 변수는 “niter” 인수를 통해 검색 집합을 실행하는 반복 횟수이며 기본값은 100입니다.

수천 회 이상으로 설정할 수 있습니다.

1
2
3
...
# perform the basin hopping search
result = basinhopping(objective, pt, niter=10000)

후보 솔루션에 적용되는 섭동의 양은 문제 영역의 경계 컨텍스트에서 적용되는 최대 변경량을 정의하는 “stepsize“를 통해 제어할 수 있습니다. 기본적으로 이 값은 0.5로 설정되지만 검색에서 새 basin을 찾을 수 있도록 도메인에서 적절한 값으로 설정해야 합니다.

예를 들어 검색 공간의 합리적인 범위가 -100에서 100인 경우 단계 크기는 5.0 또는 10.0 단위(예: 도메인의 2.5% 또는 5%)가 적절할 수 있습니다.

1
2
3
...
# perform the basin hopping search
result = basinhopping(objective, pt, stepsize=10.0)

기본적으로 사용되는 로컬 검색 알고리즘은 “L-BFGS-B” 알고리즘입니다.

이는 “minimizer_kwargs” 인수를 “method” 키가 있는 디렉터리로 설정하고 값을 사용할 로컬 검색 알고리즘의 이름(예: “nelder-mead“)으로 설정하여 변경할 수 있습니다. SciPy 라이브러리에서 제공하는 모든 로컬 검색 알고리즘을 사용할 수 있습니다.

1
2
3
...
# perform the basin hopping search
result = basinhopping(objective, pt, minimizer_kwargs={‘method’:‘nelder-mead’})

검색 결과는 사전처럼 속성에 액세스할 수 있는 OptimizeResult 개체입니다. 검색의 성공 여부는 ‘성공‘또는 ‘메시지‘키를 통해 액세스 할 수 있습니다.

총 함수 평가 횟수는 ‘nfev‘를 통해 액세스할 수 있으며 검색을 위해 찾은 최적의 입력은 ‘x‘ 키를 통해 액세스할 수 있습니다.

이제 Python의 Basin hopping API에 익숙해졌으므로 몇 가지 작업 예제를 살펴보겠습니다.

Basin hopping 예제

이 섹션에서는 다중 모드 목적 함수에서 Basin hopping 알고리즘을 사용하는 몇 가지 예를 살펴보겠습니다.

다중 모드 목적 함수는 전역 최적값과 많은 국소 최적값과 같이 여러 최적값을 갖거나 동일한 목적 함수 출력값을 갖는 여러 전역 최적값을 갖는 함수입니다.

두 기능 모두에서 Basin hopping의 예를 살펴보겠습니다.

로컬 옵티마를 사용한 다중 모드 최적화

Ackley 함수는 로컬 검색이 중단될 수 있는 단일 전역 최적값과 여러 로컬 최적값을 갖는 목적 함수의 예입니다.

따라서 전역 최적화 기술이 필요합니다. 이 함수는 전역 최적값이 [0,0]이고 0.0으로 평가되는 2차원 목적 함수입니다.

아래 예제에서는 Ackley를 구현하고 전역 최적값과 다중 국소 최적값을 보여주는 3차원 표면도를 생성합니다.

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
# ackley multimodal function
from numpy import arange
from numpy import exp
from numpy import sqrt
from numpy import cos
from numpy import e
from numpy import pi
from numpy import meshgrid
from matplotlib import pyplot
from mpl_toolkits.mplot3d import Axes3D
 
# objective function
def objective(x, y):
 return –20.0 * exp(–0.2 * sqrt(0.5 * (x**2 + y**2))) – exp(0.5 * (cos(2 * pi * x) + cos(2 * pi * y))) + e + 20
 
# define range for input
r_min, r_max = –5.0, 5.0
# sample input range uniformly at 0.1 increments
xaxis = arange(r_min, r_max, 0.1)
yaxis = arange(r_min, r_max, 0.1)
# create a mesh from the axis
x, y = meshgrid(xaxis, yaxis)
# compute targets
results = objective(x, y)
# create a surface plot with the jet color scheme
figure = pyplot.figure()
axis = figure.gca(projection=‘3d’)
axis.plot_surface(x, y, results, cmap=‘jet’)
# show the plot
pyplot.show()

예제를 실행하면 방대한 수의 국소 최적값을 보여주는 Ackley 함수의 표면도가 생성됩니다.

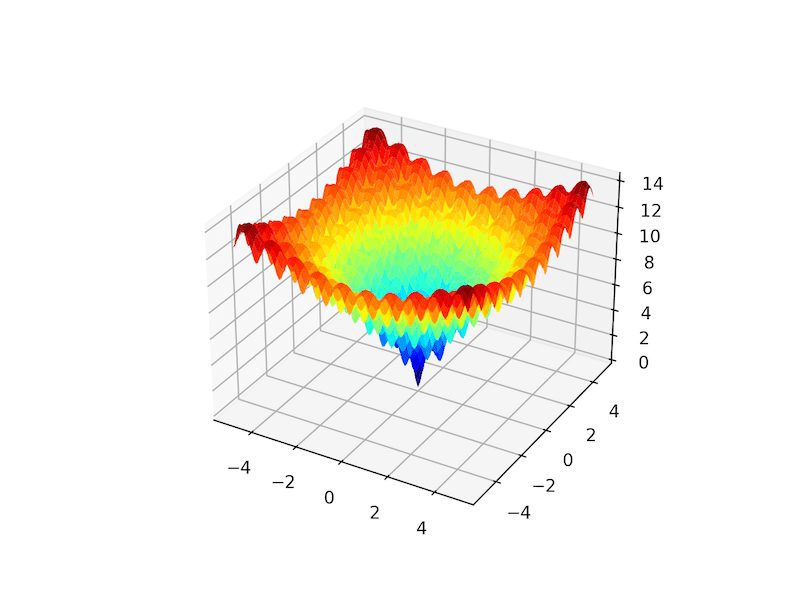
애클리 멀티모달 함수의 3D 표면도

Basin hopping 알고리즘을 Ackley 목적 함수에 적용할 수 있습니다.

이 경우 -5와 5 사이의 입력 영역에서 가져온 임의의 점을 사용하여 검색을 시작합니다.

1
2
3
...
# define the starting point as a random sample from the domain
pt = r_min + rand(2) * (r_max – r_min)

0.5의 단계 크기, 200 반복 및 기본 로컬 검색 알고리즘을 사용합니다. 이 구성은 약간의 시행 착오 후에 선택되었습니다.

1
2
3
...
# perform the basin hopping search
result = basinhopping(objective, pt, stepsize=0.5, niter=200)

검색이 완료되면 검색 상태, 수행된 반복 횟수 및 평가에서 찾은 최상의 결과를 보고합니다.

1
2
3
4
5
6
7
8
...
# summarize the result
print(‘Status : %s’ % result[‘message’])
print(‘Total Evaluations: %d’ % result[‘nfev’])
# evaluate solution
solution = result[‘x’]
evaluation = objective(solution)
print(‘Solution: f(%s) = %.5f’ % (solution, evaluation))

이를 함께 묶어 Ackley 목적 함수에 Basin hopping을 적용하는 전체 예가 아래에 나열되어 있습니다.

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
# basin hopping global optimization for the ackley multimodal objective function
from scipy.optimize import basinhopping
from numpy.random import rand
from numpy import exp
from numpy import sqrt
from numpy import cos
from numpy import e
from numpy import pi
 
# objective function
def objective(v):
 x, y = v
 return –20.0 * exp(–0.2 * sqrt(0.5 * (x**2 + y**2))) – exp(0.5 * (cos(2 * pi * x) + cos(2 * pi * y))) + e + 20
 
# define range for input
r_min, r_max = –5.0, 5.0
# define the starting point as a random sample from the domain
pt = r_min + rand(2) * (r_max – r_min)
# perform the basin hopping search
result = basinhopping(objective, pt, stepsize=0.5, niter=200)
# summarize the result
print(‘Status : %s’ % result[‘message’])
print(‘Total Evaluations: %d’ % result[‘nfev’])
# evaluate solution
solution = result[‘x’]
evaluation = objective(solution)
print(‘Solution: f(%s) = %.5f’ % (solution, evaluation))

예제를 실행하면 최적화가 실행되고 결과가 보고됩니다.

참고: 결과는 알고리즘 또는 평가 절차의 확률적 특성 또는 수치 정밀도의 차이에 따라 달라질 수 있습니다. 예제를 몇 번 실행하고 평균 결과를 비교하는 것이 좋습니다.

이 경우 알고리즘이 입력값이 0에 매우 가깝고 목적 함수 평가가 실질적으로 0인 최적값을 찾았음을 알 수 있습니다.

알고리즘을 200회 반복한 결과 86,020번의 함수 평가가 발생했음을 알 수 있습니다.

1
2
3
Status: [‘requested number of basinhopping iterations completed successfully’]
Total Evaluations: 86020
Solution: f([ 5.29778873e-10 -2.29022817e-10]) = 0.00000

다중 글로벌 최적을 사용한 다중 모드 최적화

Himmelblau 함수는 여러 개의 전역 최적값을 갖는 목적 함수의 예입니다.

구체적으로, 4개의 최적값을 가지며 각각은 동일한 목적 함수 평가를 갖습니다. [3.0, 2.0], [-2.805118, 3.131312], [-3.779310, -3.283186], [3.584428, -1.848126]에서 전체 최적값을 갖는 2차원 목적 함수입니다.

즉, 전역 최적화 알고리즘을 실행할 때마다 다른 전역 최적값을 찾을 수 있습니다.

아래 예제에서는 Himmelblau를 구현하고 목적 함수에 대한 직관을 제공하는 3차원 표면도를 생성합니다.

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
# himmelblau multimodal test function
from numpy import arange
from numpy import meshgrid
from matplotlib import pyplot
from mpl_toolkits.mplot3d import Axes3D
 
# objective function
def objective(x, y):
 return (x**2 + y – 11)**2 + (x + y**2 –7)**2
 
# define range for input
r_min, r_max = –5.0, 5.0
# sample input range uniformly at 0.1 increments
xaxis = arange(r_min, r_max, 0.1)
yaxis = arange(r_min, r_max, 0.1)
# create a mesh from the axis
x, y = meshgrid(xaxis, yaxis)
# compute targets
results = objective(x, y)
# create a surface plot with the jet color scheme
figure = pyplot.figure()
axis = figure.gca(projection=‘3d’)
axis.plot_surface(x, y, results, cmap=‘jet’)
# show the plot
pyplot.show()

예제를 실행하면 4개의 전역 최적값을 진한 파란색 분지로 표시하는 Himmelblau 함수의 표면도가 생성됩니다.

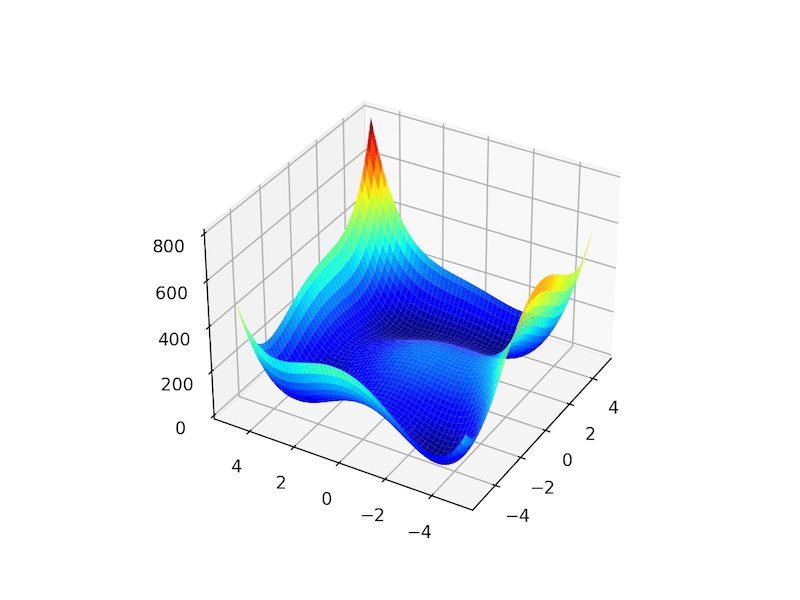
Himmelblau 다중 모드 함수의 3D 표면도

Basin hopping 알고리즘을 Himmelblau 목적 함수에 적용할 수 있습니다.

이전 예에서와 같이 -5와 5 사이의 입력 도메인에서 가져온 임의의 점을 사용하여 검색을 시작합니다.

0.5의 단계 크기, 200 반복 및 기본 로컬 검색 알고리즘을 사용합니다. 검색이 끝나면 가장 잘 위치한 최적에 대한 입력을보고합니다.

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
# basin hopping global optimization for the himmelblau multimodal objective function
from scipy.optimize import basinhopping
from numpy.random import rand
 
# objective function
def objective(v):
 x, y = v
 return (x**2 + y – 11)**2 + (x + y**2 –7)**2
 
# define range for input
r_min, r_max = –5.0, 5.0
# define the starting point as a random sample from the domain
pt = r_min + rand(2) * (r_max – r_min)
# perform the basin hopping search
result = basinhopping(objective, pt, stepsize=0.5, niter=200)
# summarize the result
print(‘Status : %s’ % result[‘message’])
print(‘Total Evaluations: %d’ % result[‘nfev’])
# evaluate solution
solution = result[‘x’]
evaluation = objective(solution)
print(‘Solution: f(%s) = %.5f’ % (solution, evaluation))

예제를 실행하면 최적화가 실행되고 결과가 보고됩니다.

이 경우 알고리즘이 약 [3.0, 2.0]에서 최적값을 찾은 것을 볼 수 있습니다.

알고리즘을 200회 반복한 결과 7,660번의 함수 평가가 발생했음을 알 수 있습니다.

1
2
3
Status : [‘requested number of basinhopping iterations completed successfully’]
Total Evaluations: 7660
Solution: f([3. 1.99999999]) = 0.00000

검색을 다시 실행하면 다른 글로벌 최적값을 찾을 것으로 예상할 수 있습니다.

예를 들어, 아래에서 이전 실행과 다른 약 [-2.805118, 3.131312]에 위치한 최적값을 볼 수 있습니다.

1
2
3
Status : [‘requested number of basinhopping iterations completed successfully’]
Total Evaluations: 7636
Solution: f([-2.80511809 3.13131252]) = 0.00000

추가 정보

이 섹션에서는 더 자세히 알아보려는 경우 주제에 대한 더 많은 리소스를 제공합니다.

논문

책

에너지 경관 : 클러스터, 생체 분자 및 유리에 대한 응용, 2004.

증권 시세 표시기

기사

요약

이 자습서에서는 Basin hopping 전역 최적화 알고리즘을 발견했습니다.

특히 다음 내용을 배웠습니다.

Basin hopping 최적화는 무작위 섭동을 사용하여 basin을 점프하고 로컬 검색 알고리즘을 사용하여 각 basin을 최적화하는 글로벌 최적화입니다.
파이썬에서 Basin hopping 최적화 알고리즘 API를 사용하는 방법.
Basin hopping을 사용하여 다중 최적으로 글로벌 최적화 문제를 해결하는 예제.

Tags:

Basin Hopping Optimization,Machine learning