머신러닝을 위한 연속 확률 분포
연속 확률 변수에 대한 확률은 연속 확률 분포로 요약할 수 있습니다.
연속 확률 분포는 머신러닝, 특히 모델에 대한 수치 입력 및 출력 변수의 분포와 모델에 의한 오류 분포에서 발생합니다. 정규 연속 확률 분포에 대한 지식은 또한 많은 머신러닝 모델에 의해 수행되는 밀도 및 매개 변수 추정에서보다 일반적으로 요구됩니다.
따라서 연속 확률 분포는 응용 머신러닝에서 중요한 역할을하며 실무자가 알아야 할 몇 가지 분포가 있습니다.
이 자습서에서는 머신러닝에 사용되는 연속 확률 분포를 알아봅니다.
이 자습서를 완료하면 다음을 알 수 있습니다.
- 연속 확률 변수에 대한 결과의 확률은 계량형 확률 분포를 사용하여 요약할 수 있습니다.
- 일반적인 계량형 확률 분포에서 파라미터화, 정의 및 랜덤하게 표본을 추출하는 방법.
- 일반적인 연속 확률 분포에 대한 확률 밀도 및 누적 밀도 플롯을 만드는 방법.
튜토리얼 개요
이 자습서는 다음과 같이 네 부분으로 나뉩니다.
- 연속 확률 분포
- 정규 분포
- 지수 분포
- 파레토 분포
연속 확률 분포
랜덤 변수는 랜덤 프로세스에 의해 생성된 수량입니다.
연속 랜덤 변수는 실제 숫자 값을 갖는 랜덤 변수입니다.
계량형 랜덤 변수의 각 수치 결과에는 확률이 할당될 수 있습니다.
연속 확률 변수에 대한 사건과 확률간의 관계를 연속 확률 분포라고 하며 확률 밀도 함수 (줄여서 PDF)로 요약됩니다.
이산 확률 변수와 달리 주어진 연속 확률 변수에 대한 확률은 직접 지정할 수 없습니다. 대신 특정 결과 주변의 작은 간격에 대한 적분(곡선 아래 영역)으로 계산됩니다.
주어진 값보다 작거나 같은 사건의 확률은 누적 분포 함수 또는 줄여서 CDF로 정의됩니다. CDF의 역수를 백분율-포인트 함수라고 하며 확률보다 작거나 같은 이산 결과를 제공합니다.
- PDF : 확률 밀도 함수, 주어진 연속 결과의 확률을 반환합니다.
- CDF: 누적 분포 함수는 주어진 결과보다 작거나 같은 값의 확률을 반환합니다.
- PPF: 퍼센트 포인트 함수는 주어진 확률보다 작거나 같은 불연속 값을 반환합니다.
일반적인 연속 확률 분포가 많이 있습니다. 가장 일반적인 것은 정규 확률 분포입니다. 실질적으로 관심있는 모든 연속 확률 분포는 소위 지수 분포 군에 속하며, 이는 매개 변수화된 확률 분포 (예 : 매개 변수 값에 따라 변경되는 분포)의 모음일 뿐입니다.
연속 확률 분포는 입력 변수의 모델 분포, 모델에 의한 오류 분포 및 입력과 출력 간의 매핑을 추정 할 때 모델 자체의 머신러닝에서 중요한 역할을합니다.
다음 섹션에서는 보다 일반적인 연속 확률 분포 중 일부를 자세히 살펴보겠습니다.
정규 분포
정규 분포는 가우스 분포(Carl Friedrich Gauss의 이름을 따서 명명됨) 또는 종 곡선 분포라고도 합니다.
분포는 다양한 문제 영역의 실제 값 사건의 확률을 다루므로 일반적이고 잘 알려진 분포이므로 “정규”라는 이름이 붙습니다. 정규 분포를 갖는 계량형 랜덤 변수를 “정규 분포” 또는 “정규 분포“라고 합니다.
정상적으로 분산된 이벤트가 있는 영역의 몇 가지 예는 다음과 같습니다.
- 사람들의 키.
- 아기의 무게.
- 시험의 점수입니다.
분포는 두 개의 매개 변수를 사용하여 정의할 수 있습니다.
- 평균(mu): 예상 값입니다.
- 분산(시그마^2): 평균으로부터의 산포.
종종 분산의 제곱근으로 계산되는 분산 대신 표준 편차가 사용됩니다(예: 정규화).
- 표준 편차(시그마): 평균으로부터의 평균 산포.
평균이 0이고 표준 편차가 1인 분포를 표준 정규 분포라고 하며, 해석 및 비교의 용이성을 위해 분석을 위해 데이터를 축소하거나 “표준화“하는 경우가 많습니다.
평균이 50이고 표준 편차가 5인 분포를 정의하고 이 분포에서 난수를 샘플링할 수 있습니다. normal() NumPy 함수를 사용하여 이를 달성할 수 있습니다.
아래 예제에서는 이 분포에서 10개의 숫자를 샘플링하고 인쇄합니다.
예제를 실행하면 정의된 정규 분포에서 랜덤하게 샘플링된 숫자 10개가 인쇄됩니다.
데이터 표본을 플로팅하고 익숙한 법선 모양을 확인하거나 통계 검정을 사용하여 랜덤인지 확인할 수 있습니다. 랜덤 변수의 관측치 표본이 정규 분포를 따르는 경우 표본에 대해 직접 계산된 평균과 분산만으로 요약할 수 있습니다.
확률 밀도 함수를 사용하여 각 관측치의 확률을 계산할 수 있습니다. 이러한 값의 플롯은 우리에게 종 모양을 보여줄 것입니다.
norm() SciPy 함수를 사용하여 정규 분포를 정의한 다음 모멘트, PDF, CDF 등과 같은 속성을 계산할 수 있습니다.
아래 예제에서는 분포에서 30과 70 사이의 정수 값에 대한 확률을 계산하고 결과를 플로팅한 다음 누적 확률에 대해 동일한 작업을 수행합니다.
먼저 예제를 실행하면 [30, 70] 범위의 정수에 대한 확률이 계산되고 값과 확률로 구성된 선 그림이 생성됩니다.
이 그림은 기대값 또는 평균 50 주변에서 가장 높은 확률의 피크를 약 8%의 확률로 가우스 또는 종 모양으로 보여줍니다.
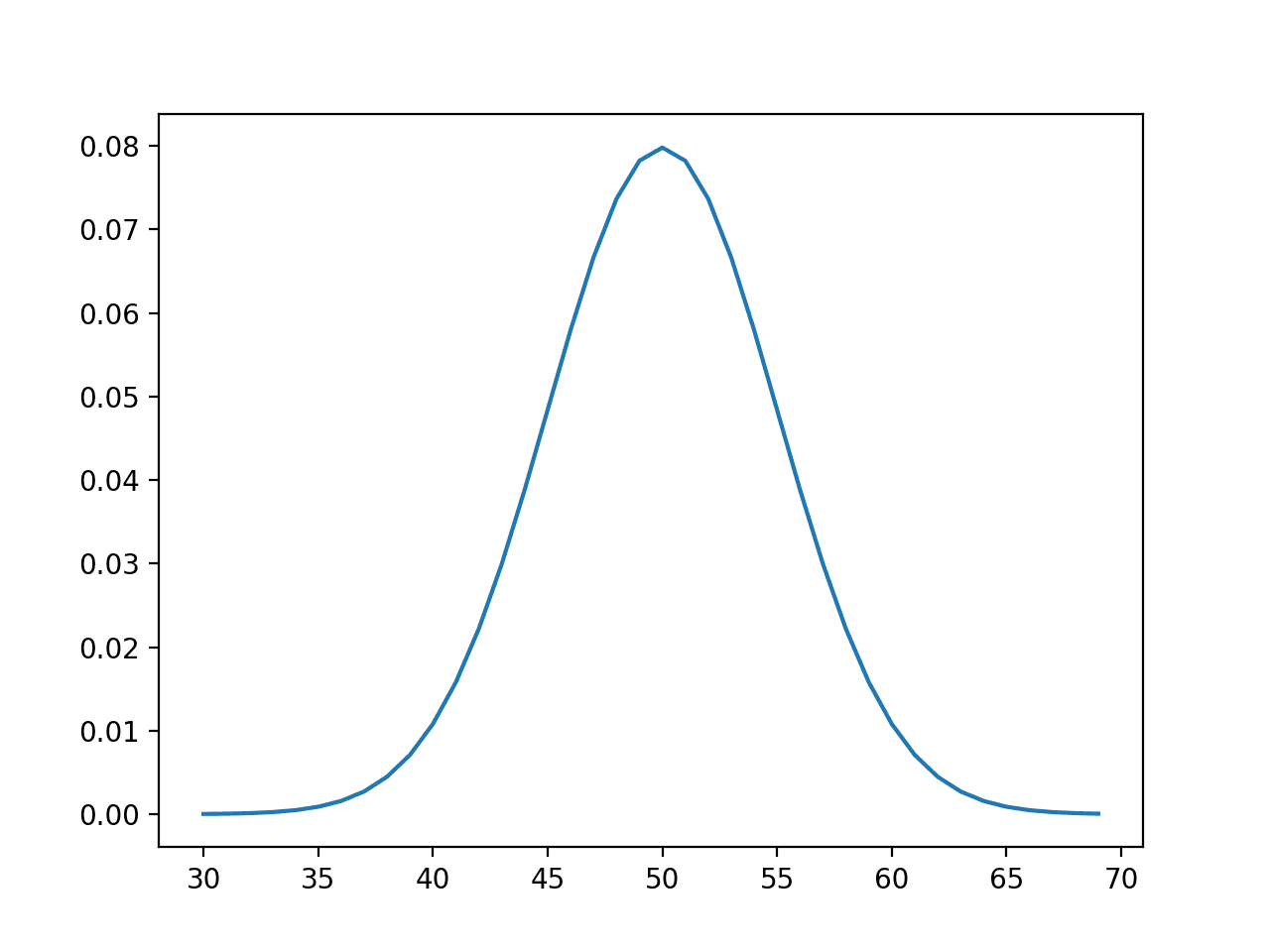
사건의 선 그림 대 확률 또는 정규 분포에 대한 확률 밀도 함수
그런 다음 동일한 범위의 관측치에 대해 누적 확률을 계산하여 평균에서 기대값의 약 50%를 포함했으며 평균에서 약 65 또는 3 표준 편차(50 + (3 * 5)) 값 이후 100%에 매우 가깝다는 것을 보여줍니다.
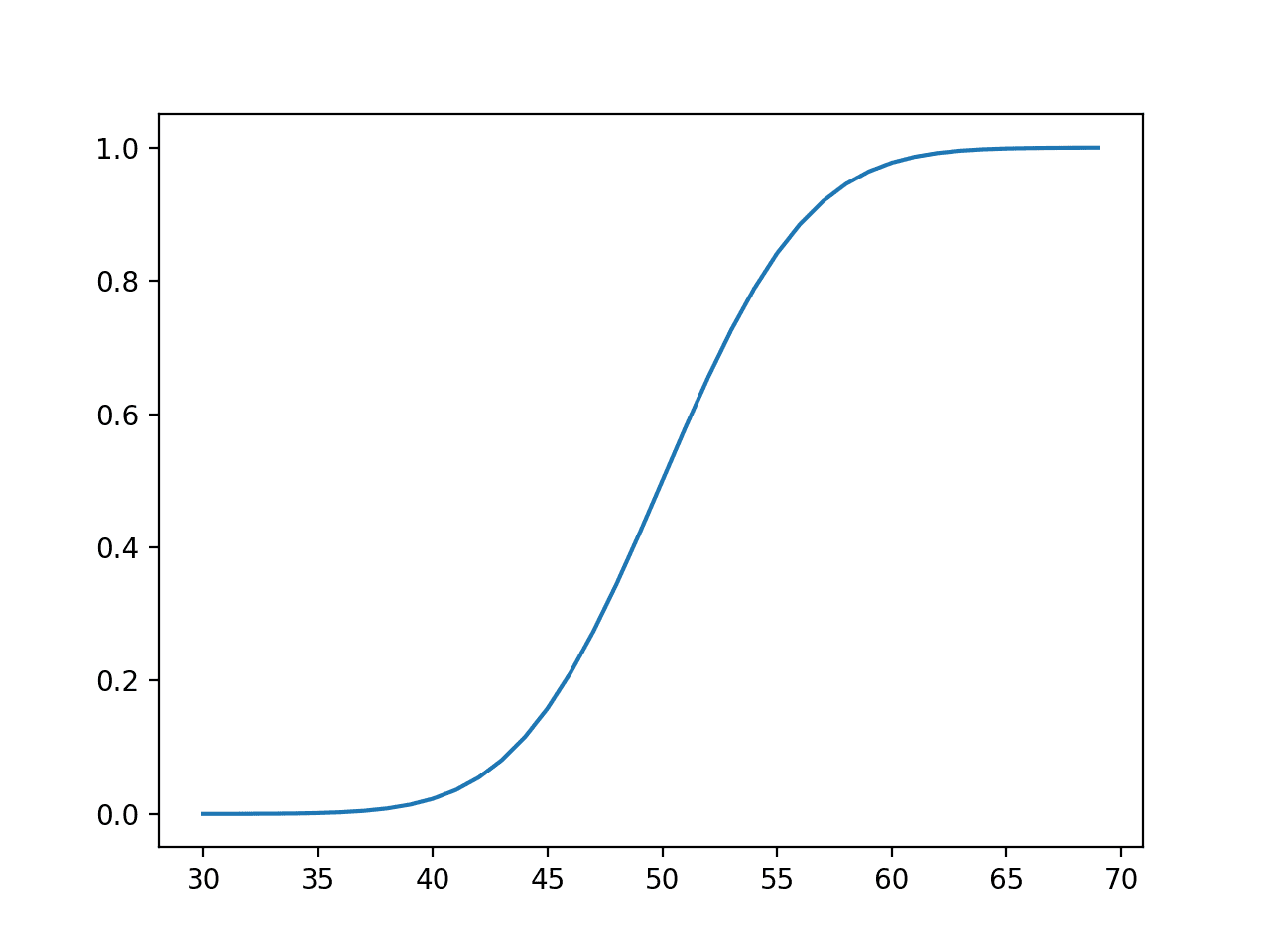
사건의 선 그림 vs. 정규 분포에 대한 누적 확률 또는 누적 밀도 함수
실제로 정규 분포에는 평균으로부터의 표준 편차 수로 지정된 범위에 포함되는 데이터의 백분율을 정의하는 휴리스틱 또는 경험 법칙이 있습니다. 이를 68-95-99.7 규칙이라고 하며, 이는 평균에서 1, 2, 3 표준 편차로 정의된 범위에 포함된 데이터의 대략적인 백분율입니다.
예를 들어, 평균이 50이고 표준 편차가 5인 분포에서 데이터의 95%가 평균에서 2 표준 편차 또는 50 – (2 * 5) 및 50 + (2 * 5) 또는 40과 60 사이의 값으로 덮일 것으로 예상합니다.
백분율 포인트 함수를 사용하여 정확한 값을 계산하여 이를 확인할 수 있습니다.
중간 95%는 저가에서 2.5%, 고가에서 97.5%에 대한 백분율 포인트 함수 값으로 정의되며, 여기서 97.5 – 2.5는 중간 95%를 제공합니다.
전체 예제는 다음과 같습니다.
예제를 실행하면 표준 편차 기반 추론 40 및 60에 매우 가까운 예상 결과의 중간 95%를 정의하는 정확한 결과를 얻을 수 있습니다.
중요한 관련 분포는로그-정규 확률 분포입니다.
지수 분포
지수분포는 몇 가지 결과가 다른 모든 결과에 비해 확률이 급격히 감소할 가능성이 가장 높은 연속 확률 분포입니다.
이산 확률 변수에 대한 기하 확률 분포와 동일한 연속 확률 변수입니다.
지수 분포 이벤트가 있는 영역의 몇 가지 예는 다음과 같습니다.
- 가이거 계수기를 클릭하는 사이의 시간입니다.
- 부품 고장까지의 시간입니다.
- 대출 불이행까지의 시간.
분포는 하나의 모수를 사용하여 정의할 수 있습니다.
- 척도(베타): 분포의 평균 및 표준 편차입니다.
때로는 분포가 매개 변수람다 또는 rate를 사용하여 더 공식적으로 정의됩니다. 베타 매개 변수는 람다 매개 변수의 역수로 정의됩니다(beta = 1/lambda)
- 비율(람다) = 분포의 변화율입니다.
평균이 50인 분포를 정의하고 이 분포에서 난수를 샘플링 할 수 있습니다. 지수() NumPy 함수를 사용하여 이를 달성할 수 있습니다.
아래 예제에서는 이 분포에서 10개의 숫자를 샘플링하고 인쇄합니다.
예제를 실행하면 정의된 분포에서 무작위로 샘플링된 10개의 숫자가 인쇄됩니다.
expon() SciPy 함수를사용하여 지수 분포를 정의한 다음 모멘트, PDF, CDF 등과 같은 속성을 계산할 수 있습니다.
아래 예제에서는 50에서 70 사이의 관측치 범위를 정의하고 각각에 대한 확률과 누적 확률을 계산하여 결과를 플로팅합니다.
먼저 예제를 실행하면 결과 대 확률의 선 그림이 생성되어 친숙한 지수 확률 분포 모양이 표시됩니다.
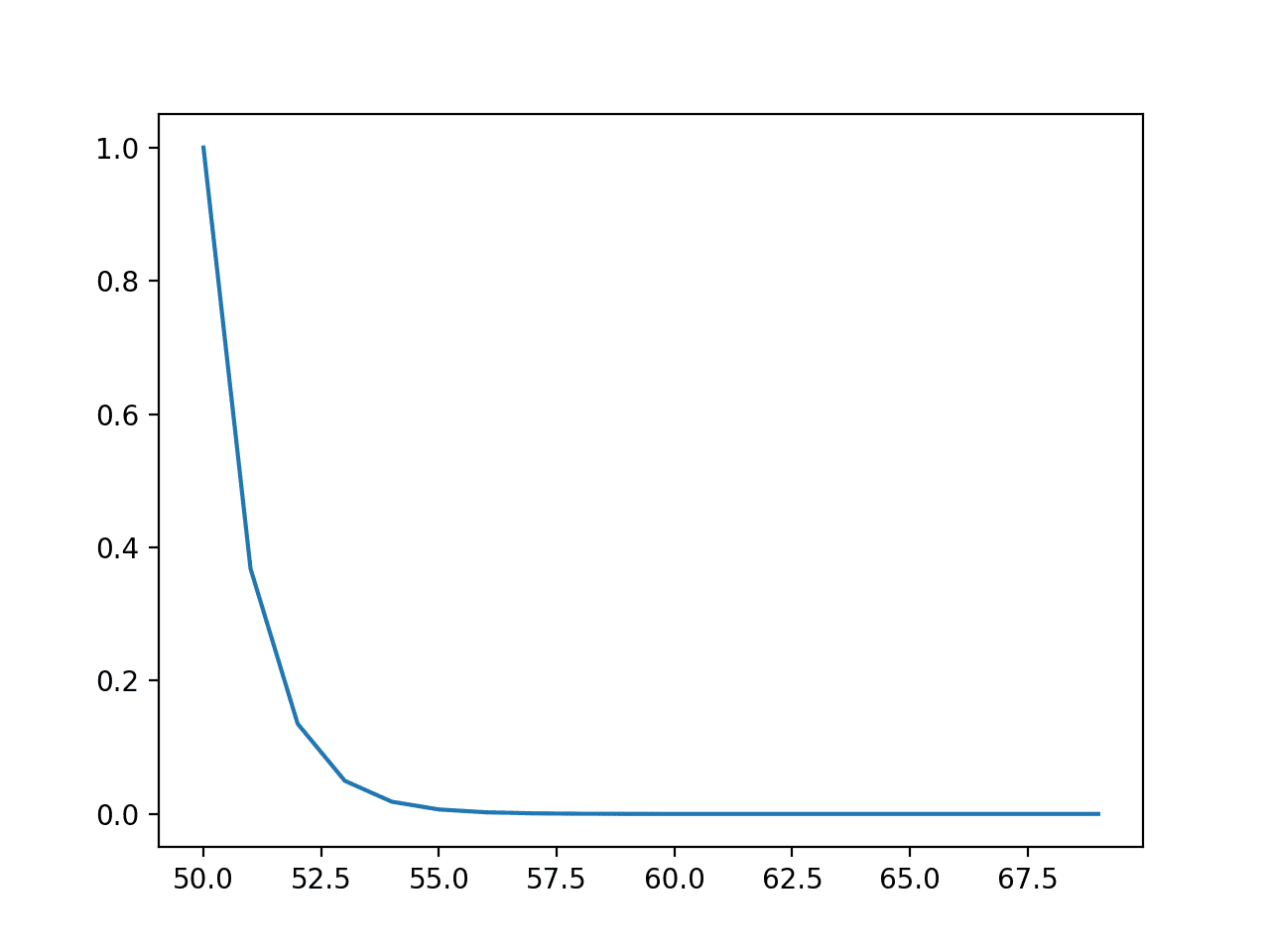
사건의 선 그림 vs. 확률 또는 지수 분포에 대한 확률 밀도 함수
다음으로, 각 결과에 대한 누적 확률이 계산되고 선 그림으로 그래프로 표시되어 55 값 이후에 예상 값의 거의 100 %가 관찰될 것임을 보여줍니다.
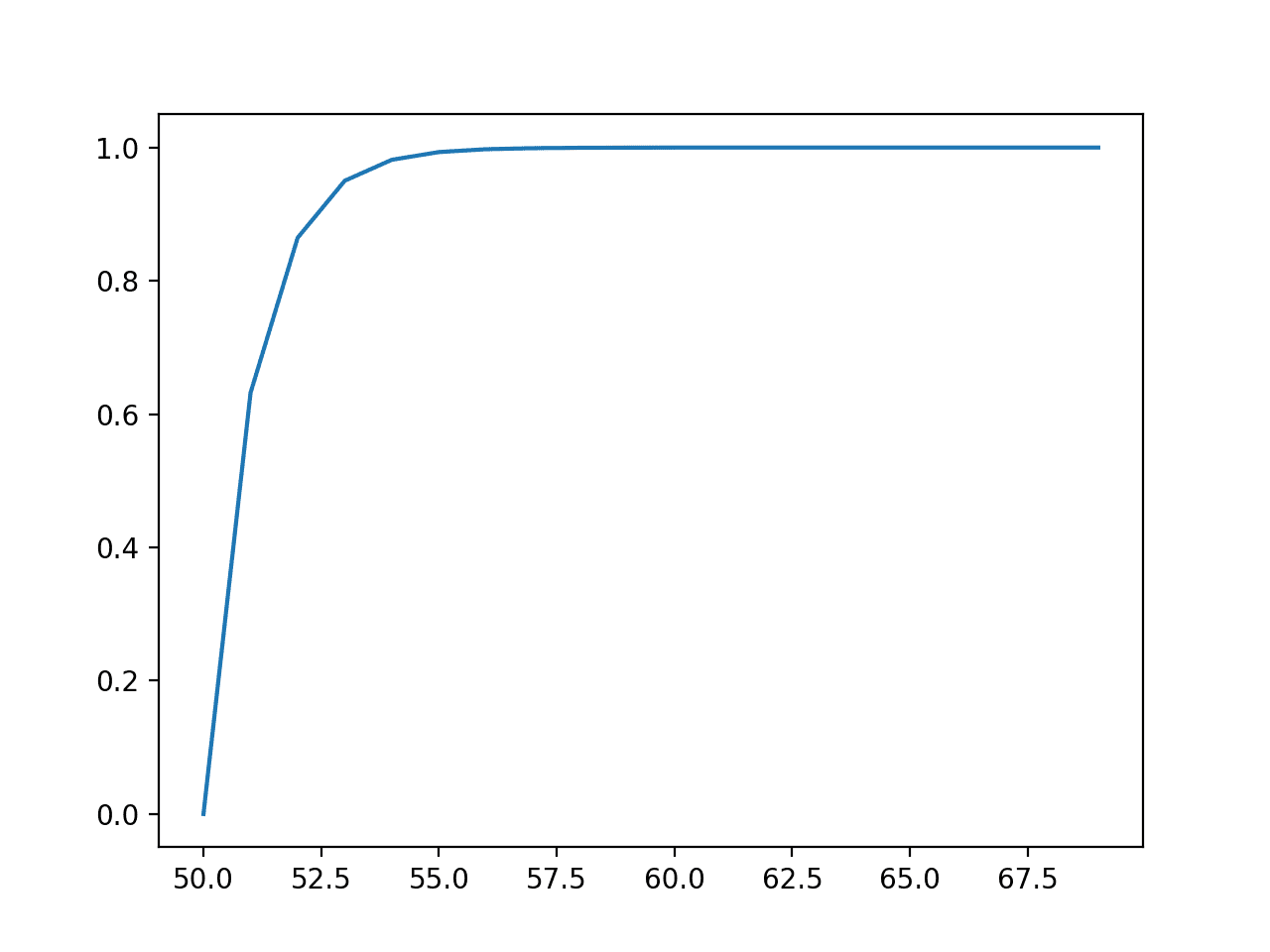
사건의 선 그림 vs. 누적 확률 또는 지수 분포에 대한 누적 밀도 함수
중요한 관련 분포는 라플라스 분포라고도 하는 이중 지수 분포입니다.
파레토 분포
파레토 분포는 빌프레도 파레토의 이름을 따서 명명되었으며 멱법칙 분포라고 할 수 있습니다.
또한 파레토 분포를 따르는 연속 확률 변수에 대한 휴리스틱 인파레토 원리 (또는 80/20 규칙)와도 관련이 있으며, 여기서 사건의 80 %는 결과 범위의 20 %로 커버됩니다 (예 : 대부분의 사건은 연속 변수 범위의 20 %에서만 추출됩니다).
파레토 법칙은 특정 파레토 분포, 특히 파레토 유형 II 분포에 대한 휴리스틱일 뿐이며, 아마도 가장 흥미롭고 우리가 집중할 것입니다.
Pareto 분산 이벤트가 있는 영역의 몇 가지 예는 다음과 같습니다.
- 한 국가의 가구 소득.
- 책의 총 판매량.
- 스포츠 팀 선수의 점수입니다.
분포는 하나의 모수를 사용하여 정의할 수 있습니다.
- 모양(알파): 확률의 감소의 가파른 정도.
shape 매개 변수의 값은 1과 3 사이와 같이 작은 경우가 많으며 알파가 1.161로 설정된 경우 Pareto 원리가 제공됩니다.
모양이 1.1인 분포를 정의하고 이 분포에서 난수를 샘플링할 수 있습니다. pareto() NumPy 함수를 사용하여 이를 달성할 수 있습니다.
예제를 실행하면 정의된 분포에서 무작위로 샘플링된 10개의 숫자가 인쇄됩니다.
pareto() SciPy 함수를사용하여 파레토 분포를 정의한 다음 모멘트, PDF, CDF 등과 같은 속성을 계산할 수 있습니다.
아래 예제에서는 1에서 약 10 사이의 관측치 범위를 정의하고 각각에 대한 확률과 누적 확률을 계산하여 결과를 플로팅합니다.
먼저 예제를 실행하면 결과 대 확률의 선 그림이 생성되어 친숙한 Pareto 확률 분포 모양이 표시됩니다.
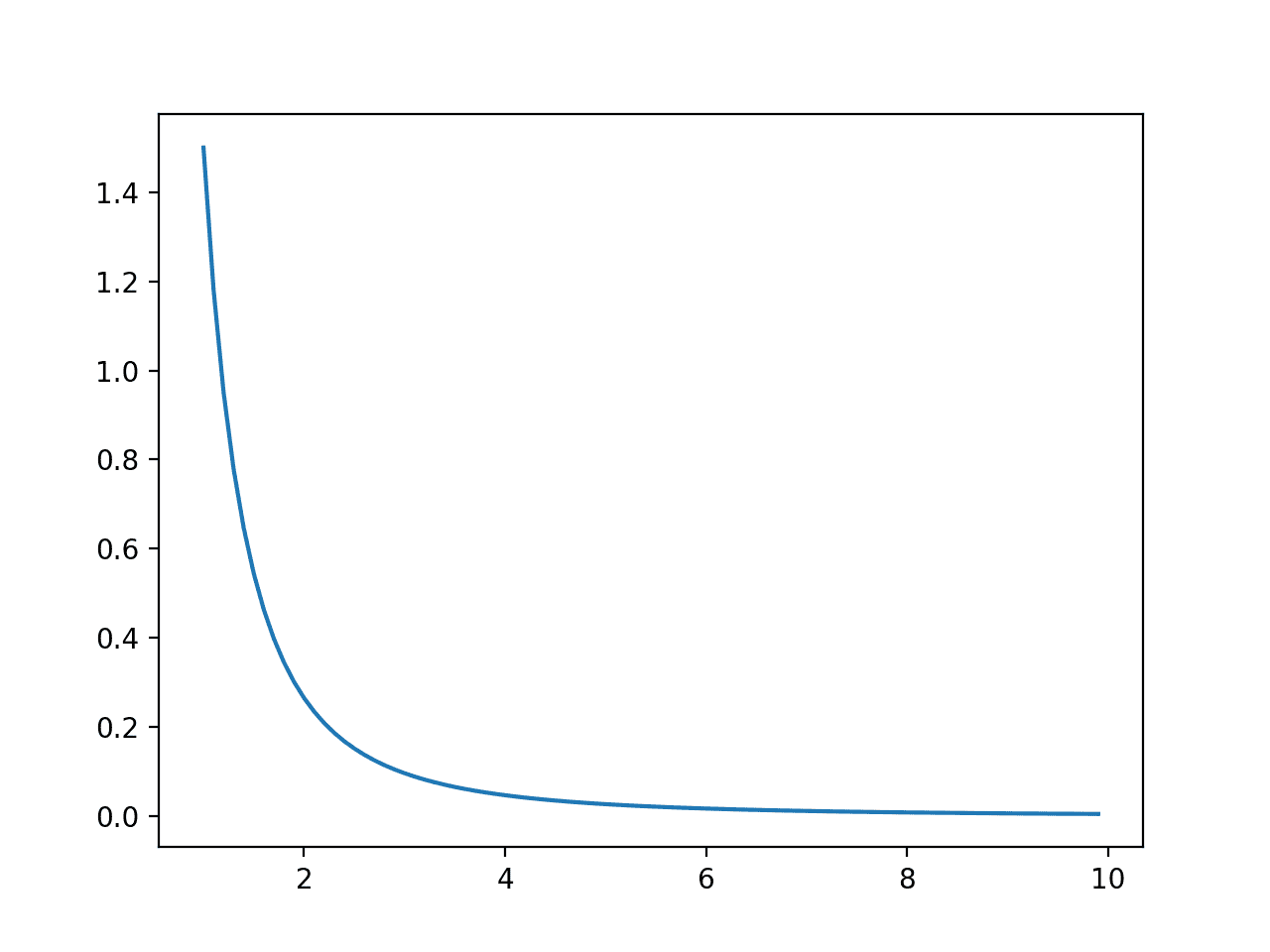
사건의 선 그림 vs. 확률 또는 파레토 분포에 대한 확률 밀도 함수
다음으로, 각 결과에 대한 누적 확률이 계산되고 선 그림으로 그래프로 표시되어 이전 섹션에서 본 지수 분포보다 덜 가파른 상승을 보여줍니다.
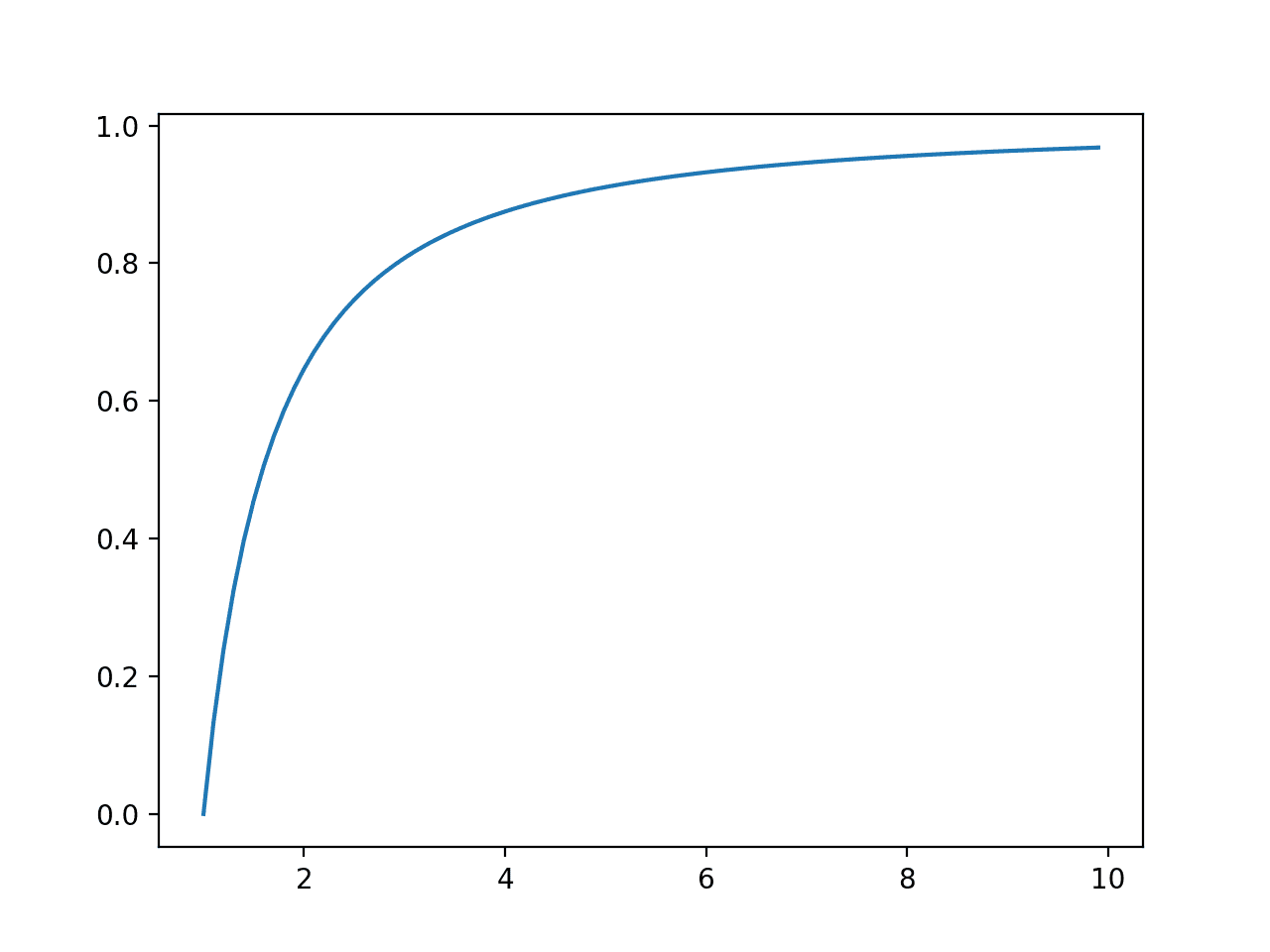
사건의 선 그림 vs. 파레토 분포에 대한 누적 확률 또는 누적 밀도 함수
추가 정보
이 섹션에서는 더 자세히 알아보려는 경우 주제에 대한 더 많은 리소스를 제공합니다.
책
- 제 2 장 : 확률 분포, 패턴 인식 및 머신러닝, 2006.
- 섹션 3.9 : 공통 확률 분포, 딥 러닝, 2016.
- 섹션 2.3 : 몇 가지 일반적인 이산 분포, 머신러닝 : 확률 론적 관점, 2012.
API
기사
요약
이 자습서에서는 머신러닝에 사용되는 연속 확률 분포를 발견했습니다.
특히 다음 내용을 배웠습니다.
- 연속 확률 변수에 대한 결과의 확률은 계량형 확률 분포를 사용하여 요약할 수 있습니다.
- 일반적인 계량형 확률 분포에서 파라미터화, 정의 및 랜덤하게 표본을 추출하는 방법.
- 일반적인 연속 확률 분포에 대한 확률 밀도 및 누적 밀도 플롯을 만드는 방법.

