머신러닝을 위한 교차 엔트로피에 대한 간략한 소개

29 11월

머신러닝을 위한 교차 엔트로피에 대한 간략한 소개

교차 엔트로피는 일반적으로 머신러닝에서 손실 함수로 사용됩니다.

교차 엔트로피는 엔트로피를 기반으로 하고 일반적으로 두 확률 분포의 차이를 계산하는 정보 이론 분야의 척도입니다. 두 확률 분포 사이의 상대 엔트로피를 계산하는 KL 발산과는 밀접한 관련이 있지만 다른 반면, 교차 엔트로피는 분포 사이의 총 엔트로피를 계산하는 것으로 생각할 수 있습니다.

교차 엔트로피는 또한 로지스틱 손실이라 불리는 로그 손실과 관련이 있으며 종종 혼동됩니다. 두 측정값이 서로 다른 소스에서 파생되었지만 분류 모델의 손실 함수로 사용되는 경우 두 측정값 모두 동일한 수량을 계산하며 서로 바꿔서 사용할 수 있습니다.

이 자습서에서는 머신러닝을 위한 교차 엔트로피를 알아봅니다.

이 자습서를 완료하면 다음을 알 수 있습니다.

교차 엔트로피를 처음부터 계산하고 표준 머신러닝 라이브러리를 사용하는 방법.
교차 엔트로피는 로지스틱 회귀 및 인공 신경망과 같은 분류 모델을 최적화할 때 손실 함수로 사용할 수 있습니다.
교차 엔트로피는 KL 발산과 다르지만 KL 발산을 사용하여 계산할 수 있으며 로그 손실과 다르지만 손실 함수로 사용할 때 동일한 양을 계산합니다.

튜토리얼 개요

이 자습서는 다섯 부분으로 나뉩니다. 그들은:

교차 엔트로피 란 무엇입니까?
교차 엔트로피 대 KL 발산
교차 엔트로피를 계산하는 방법
1. 두 개의 이산 확률 분포
2. 분포 간 교차 엔트로피 계산
3. 분포와 자체 간의 교차 엔트로피 계산
4. KL 발산을 사용한 교차 엔트로피 계산
손실 함수로서의 교차 엔트로피
1. 클래스 레이블에 대한 엔트로피 계산
2. 클래스 레이블과 확률 간의 교차 엔트로피 계산
3. Keras를 사용하여 교차 엔트로피 계산
4. 예측 확률에 대한 교차 엔트로피 직관
교차 엔트로피 대 로그 손실

로그 손실은 음의 로그 가능성입니다.
로그 손실과 교차 엔트로피는 같은 것을 계산합니다.

교차 엔트로피 란 무엇입니까?

교차 엔트로피는 주어진 확률 변수 또는 사건 집합에 대한 두 확률 분포 간의 차이를 측정한 것입니다.

이 정보는 이벤트를 인코딩하고 전송하는 데 필요한 비트 수를 수량화한다는 것을 기억할 수 있습니다. 확률이 낮은 이벤트는 더 많은 정보를 가지며 높은 확률의 이벤트는 더 적은 정보를 갖습니다.

정보 이론에서 우리는 사건의 “놀라움“을 묘사하는 것을 좋아합니다. 이벤트는 가능성이 낮을수록 더 놀라며, 이는 더 많은 정보를 포함하고 있음을 의미합니다.

낮은 확률의 사건(놀라운): 추가 정보.
더 높은 확률의 사건(놀랍지 않음): 정보가 적습니다.

정보h(x)는 다음과 같이 사건 P(x)의 확률이 주어지면 사건 x에 대해 계산할 수 있습니다.

h(x) = -log(P(x))

엔트로피는 확률 분포에서 무작위로 선택된 이벤트를 전송하는 데 필요한 비트 수입니다. 치우친 분포는 엔트로피가 낮은 반면, 사건의 확률이 동일한 분포는 엔트로피가 더 큽니다.

편향된 확률 분포는 “놀라움”이 적고 가능성이 있는 사건이 지배적이기 때문에 엔트로피가 낮습니다. 균형 분포는 더 놀랍고 사건이 똑같이 가능성이 있기 때문에 회전은 더 높은 엔트로피를 갖습니다.

비뚤어진 확률 분포(놀랍지 않음): 낮은 엔트로피.
균형 확률 분포 (놀라운) : 높은 엔트로피.

엔트로피 H(x)는 다음과 같이 X이산 상태의 x 집합과 확률P(x)를 갖는 랜덤 변수에 대해 계산할 수 있습니다.

H (X) = – X P의 합계 x P (x) * 로그 (P (x))

이벤트에 대한 정보 계산 및 분포에 대한 엔트로피에 대해 자세히 알고 싶다면 이 자습서를 참조하십시오.

정보 엔트로피에 대한 간략한 소개

교차 엔트로피는 정보 이론의 엔트로피 아이디어를 기반으로 하며 한 분포에서 다른 분포와 비교하여 평균 이벤트를 나타내거나 전송하는 데 필요한 비트 수를 계산합니다.

… 교차 엔트로피는 모델 Q를 사용할 때 분포 P가 있는 소스에서 오는 데이터를 인코딩하는 데 필요한 평균 비트 수입니다.

— 페이지 57, 머신러닝: 확률론적 관점, 2012.

이 정의에 대한 직관은 목표 또는 기본 확률 분포 P와 목표 분포 Q의 근사치를 고려하면 P에서 Q의 교차 엔트로피는 P 대신 Q를 사용하여 이벤트를 나타내는 추가 비트 수입니다.

P의 Q와 같은 두 확률 분포 사이의 교차 엔트로피는 공식적으로 다음과 같이 나타낼 수 있습니다.

H(P, Q)

여기서 H()는 교차 엔트로피 함수이고, P는 목표 분포일 수 있으며, Q는 목표 분포의 근사치입니다.

교차 엔트로피는 다음과 같이 P와 Q의 이벤트 확률을 사용하여 계산할 수 있습니다.

H (P, Q) = – X P의 합계 x P (x) * 로그 (Q (x))

여기서 P(x)는 P에 있는 사건 x의 확률이고, Q(x)는 Q에서 사건 x의 확률이며, log는 밑이 2인 로그로, 결과가 비트 단위임을 의미합니다. 밑수 e 또는 자연 로그를 대신 사용하면 결과에 nats라는 단위가 있습니다.

이 계산은 이산 확률 분포에 대한 것이지만 합계 대신 사건 전체에 걸쳐 적분을 사용하는 연속 확률 분포에도 유사한 계산을 사용할 수 있습니다.

결과는 비트 단위로 측정된 양수가 되며 두 확률 분포가 동일한 경우 분포의 엔트로피와 같습니다.

참고 :이 표기법은 결합 확률, 또는 보다 구체적으로 P와 Q 사이의 결합 엔트로피와 매우 유사합니다. 이것은 교차 엔트로피가 있는 확률 분포의 차이를 채점하기 때문에 오해의 소지가 있습니다. 반면 결합 엔트로피는 동일한 표기법을 사용하고 대신 두 개(또는 그 이상)의 확률 변수에 걸쳐 불확실성을 계산하는 다른 개념입니다.

교차 엔트로피 대 KL 발산

교차 엔트로피는 KL 발산이 아닙니다.

교차 엔트로피는 한 분포가 다른 분포와 얼마나 다른지를 정량화하는 Kullback-Leibler 또는 KL, Divergence와 같은 발산 측정과 관련이 있습니다.

특히, KL 발산은 교차 엔트로피와 매우 유사한 양을 측정합니다. 총 비트 수가 아닌 P 대신 Q로 메시지를 나타내는 데 필요한 평균 추가 비트 수를 측정합니다.

즉, KL 발산은 데이터를 인코딩하는 데 필요한 평균 추가 비트 수로, 실제 분포 p 대신 분포 q를 사용하여 데이터를 인코딩했기 때문입니다.

— 페이지 58, 머신러닝: 확률론적 관점, 2012.

따라서 KL 발산은 종종 “상대 엔트로피“라고합니다.

교차 엔트로피: P 대신 Q의 이벤트를 나타내는 총 비트의 평균 수입니다.
상대 엔트로피(KL 발산): P 대신 Q의 이벤트를 나타내는 평균 추가 비트 수입니다.

KL 발산은 P에서의 사건 확률에 대한 Q에서의 사건 확률의 로그에 의해 P 배수에서 각 사건의 확률의 음의 합으로 계산할 수 있다.

KL(P || Q) = – X P(x) * log(Q(x) / P(x))의 합계 x

합계 내의 값은 주어진 사건에 대한 발산입니다.

따라서 분포의 엔트로피와 KL 발산으로 계산 된 추가 엔트로피를 추가하여 교차 엔트로피를 계산할 수 있습니다. 이것은 두 계산의 정의를 고려할 때 직관적입니다. 예를 들어:

H(P, Q) = H(P) + KL(P || Q)

여기서 H(P, Q)는 P에서 Q의 교차 엔트로피이고, H(P)는 P와 KL(P || Q)는 P에서 Q의 발산입니다.

엔트로피는 각 이벤트에 대한 확률의 음의 합에 이벤트 확률의 로그를 곱한 값으로 확률 분포에 대해 계산할 수 있으며, 여기서 log는 결과가 비트 단위가 되도록 하기 위해 밑이 2입니다.

H (P) = – X p (x)의 합계 x * 로그 (p (x))

KL 발산과 마찬가지로 교차 엔트로피는 대칭이 아니며 다음을 의미합니다.

H(P, Q) != H(Q, P)

나중에 보게 되겠지만, 교차 엔트로피와 KL 발산은 분류 예측 모델을 최적화하기 위한 손실 함수로 사용될 때 동일한 양을 계산합니다. 이러한 맥락에서 교차 엔트로피와 KL 발산이 동일하다는 것을 때때로 알 수 있습니다.

KL 분기에 대한 자세한 내용은 자습서를 참조하십시오.

머신러닝에 대한 KL 발산을 계산하는 방법

교차 엔트로피를 계산하는 방법

이 섹션에서는 작은 예를 통해 교차 엔트로피 콘크리트를 계산할 것입니다.

두 개의 이산 확률 분포

세 개의 불연속 사건이 서로 다른 색(빨강, 녹색, 파랑)으로 있는 랜덤 변수를 고려해 보십시오.

이 변수에 대해 두 가지 다른 확률 분포가있을 수 있습니다. 예를 들어:

1
2
3
4
5
...
# define distributions
events = [‘red’, ‘green’, ‘blue’]
p = [0.10, 0.40, 0.50]
q = [0.80, 0.15, 0.05]

이러한 확률의 막대 차트를 플로팅하여 확률 히스토그램으로 직접 비교할 수 있습니다.

전체 예제는 다음과 같습니다.

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
# plot of distributions
from matplotlib import pyplot
# define distributions
events = [‘red’, ‘green’, ‘blue’]
p = [0.10, 0.40, 0.50]
q = [0.80, 0.15, 0.05]
print(‘P=%.3f Q=%.3f’ % (sum(p), sum(q)))
# plot first distribution
pyplot.subplot(2,1,1)
pyplot.bar(events, p)
# plot second distribution
pyplot.subplot(2,1,2)
pyplot.bar(events, q)
# show the plot
pyplot.show()

예제를 실행하면 각 확률 분포에 대한 히스토그램이 생성되어 각 사건의 확률을 직접 비교할 수 있습니다.

실제로 분포가 다르다는 것을 알 수 있습니다.

동일한 랜덤 변수에 대한 두 개의 서로 다른 확률 분포의 히스토그램

분포 간 교차 엔트로피 계산

다음으로 두 분포 간의 교차 엔트로피를 계산하는 함수를 개발할 수 있습니다.

log base-2를 사용하여 결과에 비트 단위의 단위가 있는지 확인합니다.

1
2
3
# calculate cross entropy
def cross_entropy(p, q):
	return –sum([p[i]*log2(q[i]) for i in range(len(p))])

그런 다음이 함수를 사용하여 Q에서 P의 교차 엔트로피를 계산하고 P에서 그 반대의 Q를 계산할 수 있습니다.

1
2
3
4
5
6
7
...
# calculate cross entropy H(P, Q)
ce_pq = cross_entropy(p, q)
print(‘H(P, Q): %.3f bits’ % ce_pq)
# calculate cross entropy H(Q, P)
ce_qp = cross_entropy(q, p)
print(‘H(Q, P): %.3f bits’ % ce_qp)

이 모든 것을 함께 묶어 전체 예제가 아래에 나열되어 있습니다.

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
# example of calculating cross entropy
from math import log2
 
# calculate cross entropy
def cross_entropy(p, q):
	return –sum([p[i]*log2(q[i]) for i in range(len(p))])
 
# define data
p = [0.10, 0.40, 0.50]
q = [0.80, 0.15, 0.05]
# calculate cross entropy H(P, Q)
ce_pq = cross_entropy(p, q)
print(‘H(P, Q): %.3f bits’ % ce_pq)
# calculate cross entropy H(Q, P)
ce_qp = cross_entropy(q, p)
print(‘H(Q, P): %.3f bits’ % ce_qp)

예제를 실행하면 먼저 P에서 Q의 교차 엔트로피가 3비트를 약간 넘은 것으로 계산한 다음 Q에서 P의 교차 엔트로피를 3비트 미만으로 계산합니다.

1
2
H(P, Q): 3.288 bits
H(Q, P): 2.906 bits

분포와 자체 간의 교차 엔트로피 계산

두 확률 분포가 같으면 두 확률 분포 사이의 교차 엔트로피가 분포의 엔트로피가됩니다.

P 대 P 및 Q 대 Q의 교차 엔트로피를 계산하여이를 입증 할 수 있습니다.

전체 예제는 다음과 같습니다.

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
# example of calculating cross entropy for identical distributions
from math import log2
 
# calculate cross entropy
def cross_entropy(p, q):
	return –sum([p[i]*log2(q[i]) for i in range(len(p))])
 
# define data
p = [0.10, 0.40, 0.50]
q = [0.80, 0.15, 0.05]
# calculate cross entropy H(P, P)
ce_pp = cross_entropy(p, p)
print(‘H(P, P): %.3f bits’ % ce_pp)
# calculate cross entropy H(Q, Q)
ce_qq = cross_entropy(q, q)
print(‘H(Q, Q): %.3f bits’ % ce_qq)

예제를 실행하면 먼저 Q에 대한 엔트로피로 계산되는 Q 대 Q의 교차 엔트로피와 P에 대한 엔트로피로 계산되는 P 대 P의 교차 엔트로피가 계산됩니다.

1
2
H(P, P): 1.361 bits
H(Q, Q): 0.884 bits

KL 발산을 사용한 교차 엔트로피 계산

KL 발산을 사용하여 교차 엔트로피를 계산할 수도 있습니다.

KL 발산으로 계산 된 교차 엔트로피는 동일해야하며, 교차 엔트로피에 의해 계산 된 총 비트 대신 필요한 상대 엔트로피 또는 추가 비트를 확인하기 위해 분포 간의 KL 발산을 계산하는 것도 흥미로울 수 있습니다.

먼저, 로그 base-2를 사용하여 분포 간의 KL 발산을 계산하는 함수를 정의하여 결과도 비트 단위가 되도록 할 수 있습니다.

1
2
3
# calculate the kl divergence KL(P || Q)
def kl_divergence(p, q):
	return sum(p[i] * log2(p[i]/q[i]) for i in range(len(p)))

다음으로 주어진 확률 분포에 대한 엔트로피를 계산하는 함수를 정의할 수 있습니다.

1
2
3
# calculate entropy H(P)
def entropy(p):
	return –sum([p[i] * log2(p[i]) for i in range(len(p))])

마지막으로 엔트로피() 및kl_divergence() 함수를 사용하여 교차엔트로피를 계산할 수 있습니다.

1
2
3
# calculate cross entropy H(P, Q)
def cross_entropy(p, q):
	return entropy(p) + kl_divergence(p, q)

예제를 간단하게 유지하기 위해 H (P, Q)에 대한 교차 엔트로피를 KL 발산 KL (P || Q) 및 엔트로피 H(P).

전체 예제는 다음과 같습니다.

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
# example of calculating cross entropy with kl divergence
from math import log2
 
# calculate the kl divergence KL(P || Q)
def kl_divergence(p, q):
	return sum(p[i] * log2(p[i]/q[i]) for i in range(len(p)))
 
# calculate entropy H(P)
def entropy(p):
	return –sum([p[i] * log2(p[i]) for i in range(len(p))])
 
# calculate cross entropy H(P, Q)
def cross_entropy(p, q):
	return entropy(p) + kl_divergence(p, q)
 
# define data
p = [0.10, 0.40, 0.50]
q = [0.80, 0.15, 0.05]
# calculate H(P)
en_p = entropy(p)
print(‘H(P): %.3f bits’ % en_p)
# calculate kl divergence KL(P || Q)
kl_pq = kl_divergence(p, q)
print(‘KL(P || Q): %.3f bits’ % kl_pq)
# calculate cross entropy H(P, Q)
ce_pq = cross_entropy(p, q)
print(‘H(P, Q): %.3f bits’ % ce_pq)

예제를 실행하면 3.288비트의 교차 엔트로피 점수가 P 1.361의 엔트로피와 KL 발산에 의해 계산된 추가 1.927비트로 구성된다는 것을 알 수 있습니다.

이것은 세 가지 계산 모두의 관계를 명확하게 보여주는 유용한 예입니다.

1
2
3
H(P): 1.361 bits
KL(P || Q): 1.927 bits
H(P, Q): 3.288 bits

손실 함수로서의 교차 엔트로피

교차 엔트로피는 분류 모델을 최적화할 때 손실 함수로 널리 사용됩니다.

발생할 수 있는 두 가지 예로는 로지스틱 회귀 알고리즘(선형 분류 알고리즘)과 분류 작업에 사용할 수 있는 인공 신경망이 있습니다.

… 분류 문제에 제곱합 대신 교차 엔트로피 오류 함수를 사용하면 훈련 속도가 빨라지고 일반화가 향상됩니다.

— 페이지 235, 패턴 인식 및 머신러닝, 2006.

분류 문제는 하나 이상의 입력 변수와 클래스 레이블의 예측과 관련된 문제입니다.

출력 변수에 대한 레이블이 두 개뿐인 분류 작업을 이진 분류 문제라고 하는 반면, 레이블이 두 개 이상인 분류 작업을 범주 또는 다중 클래스 분류 문제라고 합니다.

이진 분류: 지정된 예제에 대한 두 클래스 레이블 중 하나를 예측하는 작업입니다.
다중 클래스 분류: 지정된 예제에 대해 세 개 이상의 클래스 레이블 중 하나를 예측하는 작업입니다.

교차 엔트로피의 아이디어가 분류 모델을 최적화하는 데 유용할 수 있음을 알 수 있습니다.

각 예제에는 확률이 1.0이고 다른 모든 레이블에 대한 확률이 0.0인 알려진 클래스 레이블이 있습니다. 모델은 각 클래스 레이블에 속하는 예제의 확률을 추정할 수 있습니다. 그런 다음 교차 엔트로피를 사용하여 두 확률 분포 간의 차이를 계산할 수 있습니다.

따라서 한 예제의 분류를 다음과 같이 확률 분포를 가진 확률 변수의 아이디어에 매핑 할 수 있습니다.

랜덤 변수: 예측된 클래스 레이블이 필요한 예제입니다.
이벤트: 예측할 수 있는 각 클래스 레이블입니다.

분류 작업에서 입력값에 대한 목표 확률 분포 P를 클래스 레이블 0 또는 1로 알고 확률로 각각 “불가능” 또는 “확실“로 해석됩니다. 이러한 확률은 전혀 놀라운 일이 아니므로 정보 내용이 없거나 엔트로피가 0입니다.

이 모델은 목표 확률 분포 Q를 근사화하려고 합니다.

분류 언어에서 이들은 실제 확률과 예측 확률 또는 y와 yhat입니다.

기대 확률(y): 데이터 세트의 예제에 대한 각 클래스 레이블의 알려진 확률(P)입니다.
예측 확률(yhat): 각 클래스가 모델에 의해 예측된 예제에 레이블을 지정할 확률(Q)입니다.

따라서 위에서 설명한 교차 엔트로피 계산을 사용하여 단일 예측에 대한 교차 엔트로피를 추정할 수 있습니다. 예를 들어.

H (P, Q) = – X P의 합계 x P (x) * 로그 (Q (x))

여기서X의 각 x는 예제에 할당할 수 있는 클래스 레이블이고 P(x)는 알려진 레이블의 경우 1이고 다른 모든 레이블의 경우 0입니다.

이진 분류 작업의 단일 예제에 대한 교차 엔트로피는 다음과 같이 합계 연산을 풀어서 나타낼 수 있습니다.

H(P, Q) = – (P(class0) * log(Q(class0)) + P(class1) * log(Q(class1)))

교과서에서 인용된 교차 엔트로피 계산의 이러한 형태를 볼 수 있습니다.

클래스 레이블이 두개 뿐인 경우 확률은 양수 클래스 레이블에 대한 Bernoulli 분포로 모델링됩니다. 즉, 클래스 1에 대한 확률은 모델에 의해 직접 예측되고 클래스 0에 대한 확률은 1에서 예측 확률을 뺀 값으로 제공됩니다.

예측 P(클래스0)= 1 – yhat
예측 P(클래스1)= yhat

분류 작업에 대한 교차 엔트로피를 계산할 때 base-e 또는 자연 로그가 사용됩니다. 이것은 단위가 비트가 아닌 nats에 있음을 의미합니다.

우리는 종종 전체 학습 데이터 세트에서 모델의 교차 엔트로피를 최소화하는 데 관심이 있습니다. 이는 모든 훈련 예제에서 평균 교차 엔트로피를 계산하여 계산됩니다.

클래스 레이블에 대한 엔트로피 계산

두 분포가 동일할 때 두 분포 사이의 교차 엔트로피는 확률 분포의 엔트로피와 같습니다.

클래스 레이블은 분류 작업을 위해 데이터를 준비할 때 값 0과 1을 사용하여 인코딩 됩니다.

예를 들어, 분류 문제에 세 개의 클래스가 있고 예제에 첫 번째 클래스에 대한 레이블이 있는 경우 확률 분포는 [1, 0, 0]이 됩니다. 예제에 두 번째 클래스에 대한 레이블이 있는 경우 두 이벤트에 대한 확률 분포는 [0, 1, 0]입니다. 이를원 핫 인코딩이라고 합니다.

이 확률 분포는 결과가 확실하므로 정보가 없습니다. 우리는 수업을 알고 있습니다. 따라서 이 변수의 엔트로피는 0입니다.

이것은 중요한 개념이며 작업 된 예를 통해 설명 할 수 있습니다.

3 개의 클래스가 있는 분류 문제가 있는 척하고 각 클래스에 속하는 하나의 예가 있습니다. 각 예제를 이산 확률 분포로 나타낼 수 있으며 예제가 속한 클래스에 대한 확률은 1.0이고 다른 모든 클래스에 대한 확률은 0.0입니다.

“이벤트“에서 각 “변수”에 대한 확률 분포의 엔트로피를 계산할 수 있습니다.

전체 예제는 다음과 같습니다.

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
# entropy of examples from a classification task with 3 classes
from math import log2
from numpy import asarray
 
# calculate entropy
def entropy(p):
	return –sum([p[i] * log2(p[i]) for i in range(len(p))])
 
# class 1
p = asarray([1,0,0]) + 1e–15
print(entropy(p))
# class 2
p = asarray([0,1,0]) + 1e–15
print(entropy(p))
# class 3
p = asarray([0,0,1]) + 1e–15
print(entropy(p))

예제를 실행하면 각 확률 변수에 대한 엔트로피가 계산됩니다.

각각의 경우에 엔트로피가 0.0 (실제로는 0에 매우 가까운 숫자)임을 알 수 있습니다.

0.0의 로그를 계산할 수 없으므로 log()가 망가지지 않도록 0.0 값에 매우 작은 값을 추가해야 했습니다.

1
2
3
9.805612959471341e-14
9.805612959471341e-14
9.805612959471341e-14

따라서 알려진 클래스 레이블의 엔트로피는 항상 0.0입니다.

즉, 클래스 레이블에 대해 동일한 확률 분포를 갖는 두 분포(실수 및 예측)의 교차 엔트로피도 항상 0.0이 됩니다.

학습 데이터 세트에서 교차 엔트로피를 사용하여 모델을 평가할 때 데이터 세트의 모든 예제에서 교차 엔트로피의 평균을 구합니다.

따라서 모델을 훈련할 때 교차 엔트로피 0.0은 예측된 클래스 확률이 훈련 데이터 세트의 확률과 동일하다는 것을 나타냅니다(예: 손실 0).

우리는 교차 엔트로피 대신 손실 함수처럼 KL 발산을 쉽게 최소화 할 수 있습니다.

KL 발산은 한 변수를 다른 변수와 비교하여 전송하는 데 필요한 추가 비트입니다. 클래스 레이블의 엔트로피가 없는 교차 엔트로피이며, 어쨌든 0이 될 것입니다.

따라서 분류 작업에 대한 KL 발산과 교차 엔트로피를 최소화하는 것은 동일합니다.

이 KL 발산을 최소화하는 것은 분포 간의 교차 엔트로피를 최소화하는 것과 정확히 일치합니다.

— 페이지 132,딥 러닝, 2016.

실제로 0.0의 교차 엔트로피 손실은 종종 모델이 훈련 데이터 세트에 과적합 되었음을 나타내지만 이는 또 다른 이야기입니다.

클래스 레이블과 확률 간의 교차 엔트로피 계산

분류에 교차 엔트로피를 사용하면 분류 작업의 이름을 미러링하여 클래스 수에 따라 다른 특정 이름이 제공되는 경우가 많습니다. 예를 들어:

이진 교차 엔트로피: 이진 분류 작업에 대한 손실 함수로서의 교차 엔트로피.
범주형 교차 엔트로피: 다중 클래스 분류 작업에 대한 손실 함수로서의 교차 엔트로피입니다.

우리는 작업 된 예를 통해 손실 함수 콘크리트로 교차 엔트로피를 사용할 수 있습니다.

다음 10개의 실제 클래스 레이블(P)과 예측된 클래스 레이블(Q)이 있는 2클래스 분류 작업을 고려합니다.

1
2
3
4
...
# define classification data
p = [1, 1, 1, 1, 1, 0, 0, 0, 0, 0]
q = [0.8, 0.9, 0.9, 0.6, 0.8, 0.1, 0.4, 0.2, 0.1, 0.3]

이러한 확률을 열거하고 log2() 대신 log()(자연 로그)를 사용하여 이전 섹션에서 개발한 교차 엔트로피 함수를 사용하여 각각에 대한 교차 엔트로피를 계산할 수 있습니다.

1
2
3
# calculate cross entropy
def cross_entropy(p, q):
	return –sum([p[i]*log(q[i]) for i in range(len(p))])

각 실제 및 예측 확률에 대해 예측을 각 사건의 확률 분포로 변환해야 하며, 이 경우 클래스 {0, 1}에서 클래스 0에 대한 확률과 클래스 1에 대한 확률을 뺀 값으로 변환해야 합니다.

그런 다음 교차 엔트로피를 계산하고 모든 예제에 대해 프로세스를 반복할 수 있습니다.

1
2
3
4
5
6
7
8
9
10
11
...
# calculate cross entropy for each example
results = list()
for i in range(len(p)):
	# create the distribution for each event {0, 1}
	expected = [1.0 – p[i], p[i]]
	predicted = [1.0 – q[i], q[i]]
	# calculate cross entropy for the two events
	ce = cross_entropy(expected, predicted)
	print(‘>[y=%.1f, yhat=%.1f] ce: %.3f nats’ % (p[i], q[i], ce))
	results.append(ce)

마지막으로 데이터 세트의 평균 교차 엔트로피를 계산하고 데이터 세트의 모델에 대한 교차 엔트로피 손실로 보고할 수 있습니다.

1
2
3
4
...
# calculate the average cross entropy
mean_ce = mean(results)
print(‘Average Cross Entropy: %.3f nats’ % mean_ce)

이 모든 것을 함께 묶어 전체 예제가 아래에 나열되어 있습니다.

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
# calculate cross entropy for classification problem
from math import log
from numpy import mean
 
# calculate cross entropy
def cross_entropy(p, q):
	return –sum([p[i]*log(q[i]) for i in range(len(p))])
 
# define classification data
p = [1, 1, 1, 1, 1, 0, 0, 0, 0, 0]
q = [0.8, 0.9, 0.9, 0.6, 0.8, 0.1, 0.4, 0.2, 0.1, 0.3]
# calculate cross entropy for each example
results = list()
for i in range(len(p)):
	# create the distribution for each event {0, 1}
	expected = [1.0 – p[i], p[i]]
	predicted = [1.0 – q[i], q[i]]
	# calculate cross entropy for the two events
	ce = cross_entropy(expected, predicted)
	print(‘>[y=%.1f, yhat=%.1f] ce: %.3f nats’ % (p[i], q[i], ce))
	results.append(ce)
 
# calculate the average cross entropy
mean_ce = mean(results)
print(‘Average Cross Entropy: %.3f nats’ % mean_ce)

예제를 실행하면 각 예제에 대한 실제 및 예측 확률과 nats의 교차 엔트로피가 인쇄됩니다.

모든 예제에 걸친 최종 평균 교차 엔트로피 손실은 이 경우 0.247nats로 보고됩니다.

1
2
3
4
5
6
7
8
9
10
11
>[y=1.0, yhat=0.8] ce: 0.223 nats
>[y=1.0, yhat=0.9] ce: 0.105 nats
>[y=1.0, yhat=0.9] ce: 0.105 nats
>[y=1.0, yhat=0.6] ce: 0.511 nats
>[y=1.0, yhat=0.8] ce: 0.223 nats
>[y=0.0, yhat=0.1] ce: 0.105 nats
>[y=0.0, yhat=0.4] ce: 0.511 nats
>[y=0.0, yhat=0.2] ce: 0.223 nats
>[y=0.0, yhat=0.1] ce: 0.105 nats
>[y=0.0, yhat=0.3] ce: 0.357 nats
Average Cross Entropy: 0.247 nats

이것은 교차 엔트로피 손실 함수에서 로지스틱 회귀 모델 또는 신경망 모델을 최적화 할 때 교차 엔트로피 손실이 계산되는 방법입니다.

Keras를 사용하여 교차 엔트로피 계산

Keras 딥러닝 API의 binary_crossentropy()함수를 사용하여 작은 데이터 세트에 대한 교차 엔트로피 손실을 계산하여 동일한 계산을 확인할 수 있습니다.

전체 예제는 다음과 같습니다.

참고: 이 예에서는 Keras라이브러리(예: 버전 2.3 이상)가 설치되어 있고 TensorFlow(버전 2.0 이상)와 같은 백엔드 라이브러리로 구성되어 있다고 가정합니다. 그렇지 않은 경우 이 예제 실행을 건너뛸 수 있습니다.

1
2
3
4
5
6
7
8
9
10
11
12
13
# calculate cross entropy with keras
from numpy import asarray
from keras import backend
from keras.losses import binary_crossentropy
# prepare classification data
p = asarray([1, 1, 1, 1, 1, 0, 0, 0, 0, 0])
q = asarray([0.8, 0.9, 0.9, 0.6, 0.8, 0.1, 0.4, 0.2, 0.1, 0.3])
# convert to keras variables
y_true = backend.variable(p)
y_pred = backend.variable(q)
# calculate the average cross-entropy
mean_ce = backend.eval(binary_crossentropy(y_true, y_pred))
print(‘Average Cross Entropy: %.3f nats’ % mean_ce)

예제를 실행하면 0.247nats의 동일한 평균 교차 엔트로피 손실이 보고되는 것을 볼 수 있습니다.

이것은 교차 엔트로피의 올바른 수동 계산을 확인합니다.

1
Average Cross Entropy: 0.247 nats

예측 확률에 대한 교차 엔트로피에 대한 직관

우리는 예측 된 클래스 확률에 대한 교차 엔트로피에 대한 직관을 더욱 발전시킬 수 있습니다.

예를 들어, 0.0의 평균 교차 엔트로피 손실이 완벽한 모델이라고 가정하면 0보다 큰 평균 교차 엔트로피 값은 정확히 무엇을 의미합니까?

우리는 클래스가 0과 1로 레이블이 지정되는 이진 분류 문제가 아닌 이 질문을 탐구 할 수 있습니다. 이것은 두 개의 사건과 한 사건에 대한 특정 확률과 다른 사건에 대한 불가능한 확률을 갖는 이산 확률 분포입니다.

그런 다음 목표 분포의 완벽한 일치에서 정확히 반대되는 확률 분포로 전환되는 다양한 “예측된” 확률 분포에 대한 교차 엔트로피를 계산할 수 있습니다.

예측된 확률 분포가 목표 분포에서 더 멀어짐에 따라 계산된 교차 엔트로피가 증가할 것으로 예상합니다.

아래 예제에서는 이를 구현하고 이진 분류 작업에서 교차 엔트로피에 대해 볼 수 있는 것처럼 두 이벤트에 대한 [0, 1]의 목표값과 비교하여 예측된 확률 분포에 대한 교차 엔트로피 결과를 플로팅합니다.

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
# cross-entropy for predicted probability distribution vs label
from math import log
from matplotlib import pyplot
 
# calculate cross-entropy
def cross_entropy(p, q, ets=1e–15):
	return –sum([p[i]*log(q[i]+ets) for i in range(len(p))])
 
# define the target distribution for two events
target = [0.0, 1.0]
# define probabilities for the first event
probs = [1.0, 0.9, 0.8, 0.7, 0.6, 0.5, 0.4, 0.3, 0.2, 0.1, 0.0]
# create probability distributions for the two events
dists = [[1.0 – p, p] for p in probs]
# calculate cross-entropy for each distribution
ents = [cross_entropy(target, d) for d in dists]
# plot probability distribution vs cross-entropy
pyplot.plot([1–p for p in probs], ents, marker=‘.’)
pyplot.title(‘Probability Distribution vs Cross-Entropy’)
pyplot.xticks([1–p for p in probs], [‘[%.1f,%.1f]’%(d[0],d[1]) for d in dists], rotation=70)
pyplot.subplots_adjust(bottom=0.2)
pyplot.xlabel(‘Probability Distribution’)
pyplot.ylabel(‘Cross-Entropy (nats)’)
pyplot.show()

예제를 실행하면 각 확률 분포에 대한 교차 엔트로피 점수가 계산된 다음 결과를 선 그림으로 플로팅합니다.

예상대로 교차 엔트로피는 예측 확률 분포가 목표 분포와 일치 할 때 0.0 (맨 왼쪽 지점)에서 시작하여 예측 된 확률 분포가 분기됨에 따라 꾸준히 증가한다는 것을 알 수 있습니다.

또한 예측된 확률 분포가 목표 분포와 정반대일 때, 즉 [0, 1]의 목표값과 비교하여 [1, 0]일 때 교차 엔트로피의 극적인 도약을 볼 수 있습니다.

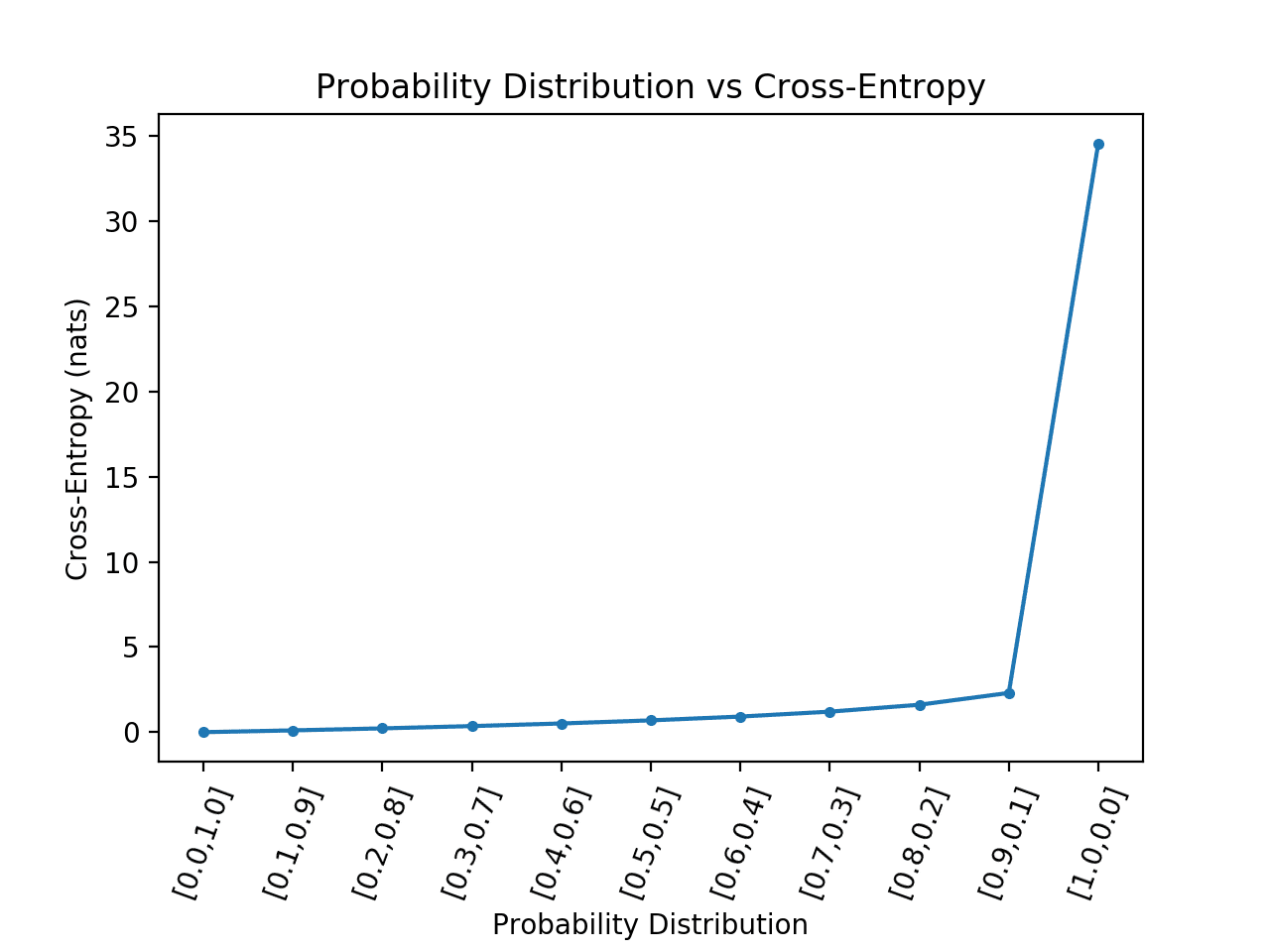
이진 분류 작업에 대한 확률 분포 대 교차 엔트로피의 선 그림

우리는 이진 분류 작업의 모든 경우에 대해 정확히 반대되는 확률 분포를 예측하는 모델을 갖지 않을 것입니다.

따라서이 경우를 제거하고 플롯을 다시 계산할 수 있습니다.

업데이트된 버전의 코드는 다음과 같습니다.

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
# cross-entropy for predicted probability distribution vs label
from math import log
from matplotlib import pyplot
 
# calculate cross-entropy
def cross_entropy(p, q, ets=1e–15):
	return –sum([p[i]*log(q[i]+ets) for i in range(len(p))])
 
# define the target distribution for two events
target = [0.0, 1.0]
# define probabilities for the first event
probs = [1.0, 0.9, 0.8, 0.7, 0.6, 0.5, 0.4, 0.3, 0.2, 0.1]
# create probability distributions for the two events
dists = [[1.0 – p, p] for p in probs]
# calculate cross-entropy for each distribution
ents = [cross_entropy(target, d) for d in dists]
# plot probability distribution vs cross-entropy
pyplot.plot([1–p for p in probs], ents, marker=‘.’)
pyplot.title(‘Probability Distribution vs Cross-Entropy’)
pyplot.xticks([1–p for p in probs], [‘[%.1f,%.1f]’%(d[0],d[1]) for d in dists], rotation=70)
pyplot.subplots_adjust(bottom=0.2)
pyplot.xlabel(‘Probability Distribution’)
pyplot.ylabel(‘Cross-Entropy (nats)’)
pyplot.show()

예제를 실행하면 확률 분포의 발산과 계산된 교차 엔트로피 간의 관계에 대한 훨씬 더 나은 아이디어를 얻을 수 있습니다.

예측된 확률 분포가 목표에서 더 많이 갈수록 교차 엔트로피의 증가가 더 큰 초선형 관계를 볼 수 있습니다.

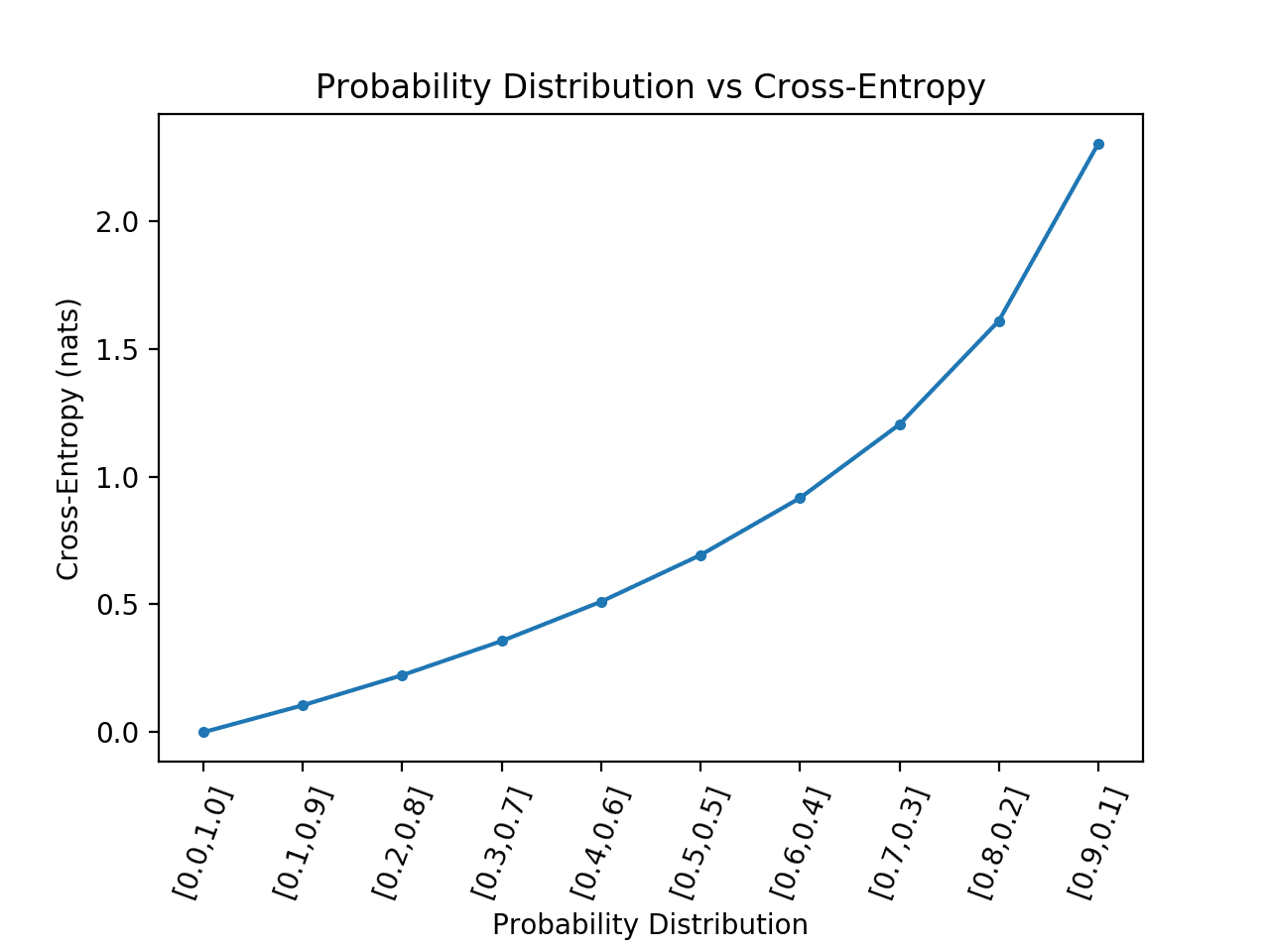
확률 분포 대 교차 엔트로피의 선 플롯 극단적 인 경우가 제거 된 이진 분류 작업

이와 같은 플롯은 이진 분류 데이터 세트의 모델에 대해 보고된 평균 교차 엔트로피를 해석하기 위한 지침으로 사용할 수 있습니다.

예를 들어 이러한 교차 엔트로피 값을 사용하여 Keras가 보고한 평균 교차 엔트로피를 이진 분류 작업의 신경망 모델 또는 logloss 메트릭을 사용하여 평가된 scikit-learn의 이진 분류 모델을 해석할 수 있습니다.

일반적인 질문에 답하는 데 사용할 수 있습니다.

좋은 교차 엔트로피 점수는 무엇입니까?

nats에서 작업 중이고 (그리고 일반적으로 그렇습니다) 평균 교차 엔트로피가 0.2보다 작 으면 좋은 출발을하고 있으며 0.1 또는 0.05보다 작 으면 더 좋습니다.

반면에 0.2 또는 0.3보다 큰 평균 교차 엔트로피를 얻으면 향상시킬 수 있으며 평균 교차 엔트로피가 1.0보다 크면 무언가가 진행되고 있으며 데이터 세트의 많은 예제에서 확률 예측이 좋지 않습니다.

평균 교차 엔트로피에 대한 이러한 직관을 다음과 같이 요약할 수 있습니다.

교차 엔트로피 = 0.00: 완벽한 확률.
교차 엔트로피 < 0.02: 큰 확률.
교차 엔트로피 < 0.05: 올바른 방향으로 가고 있습니다.
교차 엔트로피 < 0.20: 좋습니다.
교차 엔트로피 > 0.30: 좋지 않습니다.
교차 엔트로피 > 1.00: 끔찍한.
교차 엔트로피 > 2.00 뭔가 고장났습니다.

이 목록은 로지스틱 회귀 모델 또는 인공 신경망 모델에서 교차 엔트로피(로그 손실)를 해석할 때 유용한 가이드를 제공합니다.

또한 클래스별로 별도의 평균 교차 엔트로피 점수를 계산하고 모델이 좋은 확률을 가진 클래스와 엉망이 될 수있는 클래스를 파악하는 데 도움을 줄 수 있습니다.

교차 엔트로피 대 로그 손실

교차 엔트로피는 로그 손실이 아니지만 분류 문제에 대한 손실 함수로 사용될 때 동일한 양을 계산합니다.

로그 손실은 음의 로그 가능성입니다.

로지스틱 손실은 로지스틱 회귀 모델을 최적화하는 데 일반적으로 사용되는 손실 함수를 나타냅니다.

로그 손실(혼란스러움) 또는 단순히 로그 손실이라고도 합니다.

많은 모델은 관측된 데이터를 가장 잘 설명하는 매개변수 집합을 찾는 것을 포함하는 최대 발생가능성 추정(MLE)이라고 하는 확률론적 프레임워크 하에서 최적화됩니다.

여기에는 관측치(데이터) 집합에 모델 매개변수가 제공될 가능성을 정의하는 발생가능성 함수를선택하는 작업이 포함됩니다. 로그 발생가능성 함수가 사용되는 경우(일반적임) 종종 모형에 대한 로그 발생가능성 최적화라고 합니다. 실제로는 함수를 최대화하는 것보다 최소화하는 것이 더 일반적이기 때문에 로그 발생가능성 함수는 앞에 음수 부호를 추가하여 반전됩니다. 이것은 음의 로그 발생가능성 함수 또는 줄여서 NLL로 변환합니다.

베르누이 확률 분포 함수 (두 클래스)에 대한 최대 발생가능성 추정 프레임 워크 하에서 로그 발생가능성 함수를 도출 할 때 계산은 다음과 같습니다.

음의 로그 가능성(P, Q) = -(P(클래스0) * 로그(Q(클래스0)) + P(클래스1) * 로그(Q(클래스1)))

이 양은 발생가능성 함수의 로그 평균을 계산하여 모든 훈련 예제에 대해 평균을 낼 수 있습니다.

이진 분류 문제에 대한 음의 로그 발생가능성는 종종 로지스틱 회귀에 대해 파생된 손실 함수로서 단순히 “로그 손실”로 단축됩니다.

로그 손실 = 베르누이 확률 분포에서 음의 로그 발생가능성

음의 로그 발생가능성는 베르누이 확률 분포 함수(두 사건 또는 클래스)에 대한 교차 엔트로피에 사용되는 계산과 동일하다는 것을 알 수 있습니다. 사실, 다중성 분포(다중 클래스 분류)에 대한 음의 로그 발생가능성는 교차 엔트로피에 대한 계산과도 일치합니다.

로그 손실 및 음수 로그 가능성에 대한 자세한 내용은 다음 자습서를 참조하세요.

최대발생가능성 추정을 사용한 로지스틱 회귀에 대한 간략한 소개

로그 손실과 교차 엔트로피는 같은 것을 계산합니다.

분류 문제의 경우 “로그 손실“, “교차 엔트로피” 및 “음의 로그 발생가능성“가 같은 의미로 사용됩니다.

보다 일반적으로, 용어 “교차 엔트로피“와 “음의 로그 가능성“은 분류 모델에 대한 손실 함수의 맥락에서 상호 교환 적으로 사용됩니다.

로지스틱 회귀에 대한 음의 로그 발생가능성는 다음과 같이 주어집니다. 이를 교차 엔트로피 오류 함수라고도 합니다.

— 페이지 246, 머신러닝: 확률론적 관점, 2012.

따라서 로그 손실을 계산하면 베르누이 확률 분포에 대한 교차 엔트로피를 계산하는 것과 동일한 양이 제공됩니다. scikit-learn API의 log_loss() 함수를 사용하여 로그 손실을 계산하여이를 확인할 수 있습니다.

이전 섹션의 동일한 실제 및 예측 확률 집합에 대한 평균 로그 손실을 계산하면 평균 교차 엔트로피를 계산하는 것과 동일한 결과를 얻을 수 있습니다.

전체 예제는 다음과 같습니다.

1
2
3
4
5
6
7
8
9
10
11
12
# calculate log loss for classification problem with scikit-learn
from sklearn.metrics import log_loss
from numpy import asarray
# define classification data
p = [1, 1, 1, 1, 1, 0, 0, 0, 0, 0]
q = [0.8, 0.9, 0.9, 0.6, 0.8, 0.1, 0.4, 0.2, 0.1, 0.3]
# define data as expected, e.g. probability for each event {0, 1}
y_true = asarray([[1–v, v] for v in p])
y_pred = asarray([[1–v, v] for v in q])
# calculate the average log loss
ll = log_loss(y_true, y_pred)
print(‘Average Log Loss: %.3f’ % ll)

예제를 실행하면 0.247 로그 손실의 예상 결과가 제공되며, 이는 평균 교차 엔트로피를 사용하여 계산할 때 0.247nats와 일치합니다.

1
Average Log Loss: 0.247

이것은 로그 손실이 교차 엔트로피를 계산하거나 교차 엔트로피가 로그 손실을 계산한다는 것을 의미하지는 않습니다.

대신, 분류 작업에 대한 손실 함수를 계산하는 조건에서 동일한 계산 및 결과를 초래하는 서로 다른 연구 분야에서 도착한 다른 수량입니다. 특히, 교차 엔트로피 손실 함수는 베르누이 또는 다중성 확률 분포 하의 최대발생가능성 함수와 동일합니다.

이것은 최대 발생가능성 추정 연구와 이산 확률 분포에 대한 정보 이론 사이의 연관성을 보여줍니다.

이산 확률 분포에만 국한되지 않으며,이 사실은 처음 듣는 많은 실무자에게 놀랍습니다.

특히,최대 발생가능성 추정 프레임워크 하에서 최적화된 선형 회귀는 대상 변수에 대한 가우스 연속 확률 분포를 가정하고 평균 제곱 오차 함수를 최소화하는 것을 포함합니다. 이는 가우스 확률 분포를 갖는 랜덤 변수에 대한 교차 엔트로피와 동일합니다.

음의 로그 발생가능성로 구성된 모든 손실은 훈련 세트에 의해 정의된 경험적 분포와 모델에 의해 정의된 확률 분포 간의 교차 엔트로피입니다. 예를 들어, 평균 제곱 오차는 경험적 분포와 가우스 모델 간의 교차 엔트로피입니다.

— 페이지 132,딥 러닝, 2016.

이것은 약간의 마음이 불고 있으며 연속 확률 변수에 대한 미분 엔트로피분야에서 비롯됩니다.

즉, 동일한 이벤트를 포함하는 두 가우스 확률 변수 (평균 및 표준 편차가 동일 함) 간의 평균 제곱 오차를 계산하면 변수 간의 교차 엔트로피가 계산됩니다.

또한 회귀 문제에 대한 신경망 모델을 최적화하기 위해 평균 제곱 오차 손실을 사용하는 경우 사실상 교차 엔트로피 손실을 사용하고 있음을 의미합니다.

추가 정보

이 섹션에서는 더 자세히 알아보려는 경우 주제에 대한 더 많은 리소스를 제공합니다.

자습서

책

API

기사

요약

이 자습서에서는 머신러닝을 위한 교차 엔트로피를 발견했습니다.

특히 다음 내용을 배웠습니다.

교차 엔트로피를 처음부터 계산하고 표준 머신러닝 라이브러리를 사용하는 방법.
교차 엔트로피는 로지스틱 회귀 및 인공 신경망과 같은 분류 모델을 최적화할 때 손실 함수로 사용할 수 있습니다.
교차 엔트로피는 KL 발산과 다르지만 KL 발산을 사용하여 계산할 수 있으며 로그 손실과 다르지만 손실 함수로 사용할 때 동일한 양을 계산합니다.

Tags:

Cross-Entropy,Machine learning