머신러닝을 위한 행렬 및 행렬 산술 소개

13 12월

머신러닝을 위한 행렬 및 행렬 산술 소개

by Nepirity

in Technology

Comments

행렬은 선형 대수학의 기본 요소입니다.

행렬은 머신러닝 분야에서 알고리즘을 훈련할 때 입력 데이터 변수(X)와 같은 알고리즘 및 프로세스에 대한 설명에 사용됩니다.

이 튜토리얼에서는 선형 대수학의 행렬과 Python에서 이를 조작하는 방법을 알아봅니다.

이 자습서를 완료하면 다음을 알 수 있습니다.

행렬이란 무엇이며 NumPy를 사용하여 파이썬에서 행렬을 정의하는 방법.
덧셈, 뺄셈, 아다마르 곱과 같은 요소별 연산을 수행하는 방법.
행렬을 곱하는 방법과 연산 이면의 직관.

튜토리얼 개요

이 튜토리얼은 다음과 같이 여섯 부분으로 나뉩니다.

매트릭스란 무엇입니까?
행렬 정의
행렬 산술
행렬-행렬 곱셈(내적)
행렬-벡터 곱셈
행렬-스칼라 곱셈

매트릭스란 무엇입니까?

행렬은 하나 이상의 열과 하나 이상의 행이 있는 스칼라의 2차원 배열입니다.

행렬은 숫자의 2차원 배열(테이블)입니다.

— 페이지 115, 선형 대수학에 대한 좋은 가이드, 2017

행렬의 표기법은 종종 A와 같은 대문자이며 항목은 aij와 같이 행 (i) 및 열 (j)의 2차원 첨자로 참조됩니다. 예를 들어:

1
A = ((a11, a12), (a21, 22), (a31, a32))

가로 표기법을 사용하여 정의된 행렬을 보는 것이 더 일반적입니다.

1
2
3
     a11, a12
A = (a21, a22)
     a31, a32

머신러닝에서 행렬을 처음 접할 수 있는 위치는 많은 행과 열로 구성된 모델 학습 데이터이며 종종 대문자 “X”를 사용하여 표시됩니다.

벡터와 그 연산 중 일부를 이해하는 데 사용되는 기하학적 비유는 행렬과 관련이 없습니다. 또한 벡터 자체는 하나의 열과 여러 행을 갖는 행렬로 간주 될 수 있습니다.

종종 행렬의 차원은 행 수와 열 수에 대해 m과 n으로 표시됩니다.

이제 행렬이 무엇인지 알았으므로 Python에서 행렬을 정의하는 방법을 살펴보겠습니다.

행렬 정의

2 차원 NumPy 배열을 사용하여 파이썬에서 행렬을 나타낼 수 있습니다.

목록이 주어지면 NumPy 배열을 구성 할 수 있습니다. 예를 들어, 아래는 2행 3열 행렬입니다.

1
2
3
4
# create matrix
from numpy import array
A = array([[1, 2, 3], [4, 5, 6]])
print(A)

예제를 실행하면 예상되는 구조를 보여 주는 생성된 행렬이 인쇄됩니다.

1
2
[[1 2 3]
 [4 5 6]]

행렬 산술

이 섹션에서는 간단한 행렬-행렬 산술을 보여 주며, 여기서 모든 연산은 동일한 크기의 두 행렬 사이에서 요소 단위로 수행되어 동일한 크기의 새 행렬을 생성합니다.

매트릭스 추가

차원이 같은 두 행렬을 함께 추가하여 새로운 세 번째 행렬을 만들 수 있습니다.

1
C = A + B

결과 행렬의 스칼라 요소는 추가되는 각 행렬의 요소를 더한 값으로 계산됩니다.

1
2
3
         a11 + b11, a12 + b12
A + B = (a21 + b21, a22 + b22)
         a31 + b31, a32 + b32

또는 다른 방법으로 :

1
2
3
4
5
6
C[0,0] = A[0,0] + B[0,0]
C[1,0] = A[1,0] + B[1,0]
C[2,0] = A[2,0] + B[2,0]
C[0,1] = A[0,1] + B[0,1]
C[1,1] = A[1,1] + B[1,1]
C[2,1] = A[2,1] + B[2,1]

두 개의 NumPy 배열에서 직접 더하기 연산자를 사용하여 파이썬에서 이것을 구현할 수 있습니다.

1
2
3
4
5
6
7
8
# add matrices
from numpy import array
A = array([[1, 2, 3], [4, 5, 6]])
print(A)
B = array([[1, 2, 3], [4, 5, 6]])
print(B)
C = A + B
print(C)

이 예제에서는 먼저 두 개의 2×3 행렬을 정의한 다음 함께 추가합니다.

예제를 실행하면 먼저 두 부모 행렬이 인쇄된 다음 두 행렬을 함께 더한 결과가 인쇄됩니다.

1
2
3
4
5
6
7
8
[[1 2 3]
 [4 5 6]]
 
[[1 2 3]
 [4 5 6]]
 
[[ 2  4  6]
 [ 8 10 12]]

행렬 빼기

마찬가지로, 하나의 행렬은 동일한 차원을 가진 다른 행렬에서 뺄 수 있습니다.

1
C = A – B

결과 행렬의 스칼라 요소는 각 행렬의 요소를 뺀 값으로 계산됩니다.

1
2
3
         a11 – b11, a12 – b12
A – B = (a21 – b21, a22 – b22)
         a31 – b31, a32 – b32

또는 다른 방법으로 :

1
2
3
4
5
6
C[0,0] = A[0,0] – B[0,0]
C[1,0] = A[1,0] – B[1,0]
C[2,0] = A[2,0] – B[2,0]
C[0,1] = A[0,1] – B[0,1]
C[1,1] = A[1,1] – B[1,1]
C[2,1] = A[2,1] – B[2,1]

두 개의 NumPy 배열에서 직접 빼기 연산자를 사용하여 파이썬에서 이것을 구현할 수 있습니다.

1
2
3
4
5
6
7
8
# subtract matrices
from numpy import array
A = array([[1, 2, 3], [4, 5, 6]])
print(A)
B = array([[0.5, 0.5, 0.5], [0.5, 0.5, 0.5]])
print(B)
C = A – B
print(C)

이 예제에서는 먼저 두 개의 2×3 행렬을 정의한 다음 하나를 다른 행렬에서 뺍니다.

예제를 실행하면 먼저 두 개의 부모 행렬이 인쇄된 다음 두 번째 행렬에서 첫 번째 행렬을 뺍니다.

1
2
3
4
5
6
7
8
[[1 2 3]
 [4 5 6]]
 
[[ 0.5  0.5  0.5]
 [ 0.5  0.5  0.5]]
 
[[ 0.5  1.5  2.5]
 [ 3.5  4.5  5.5]]

행렬 곱셈 (하다마르 곱)

크기가 같은 두 행렬을 곱할 수 있으며 이를 요소별 행렬 곱셈 또는 아다 마르 곱이라고합니다.

행렬 곱셈을 언급 할 때 의미하는 일반적인 연산이 아니므로 원 “o”와 같은 다른 연산자가 자주 사용됩니다.

1
C = A o B

요소별 빼기 및 덧셈과 마찬가지로 요소별 곱셈은 새 행렬의 값을 계산하기 위해 각 부모 행렬의 요소를 곱하는 것을 포함합니다.

1
2
3
         a11 * b11, a12 * b12
A o B = (a21 * b21, a22 * b22)
         a31 * b31, a32 * b32

또는 다른 방법으로 :

1
2
3
4
5
6
C[0,0] = A[0,0] * B[0,0]
C[1,0] = A[1,0] * B[1,0]
C[2,0] = A[2,0] * B[2,0]
C[0,1] = A[0,1] * B[0,1]
C[1,1] = A[1,1] * B[1,1]
C[2,1] = A[2,1] * B[2,1]

두 개의 NumPy 배열에서 직접 스타 연산자를 사용하여 파이썬에서 이것을 구현할 수 있습니다.

1
2
3
4
5
6
7
8
# element-wise multiply matrices
from numpy import array
A = array([[1, 2, 3], [4, 5, 6]])
print(A)
B = array([[1, 2, 3], [4, 5, 6]])
print(B)
C = A * B
print(C)

이 예제에서는 먼저 두 개의 2×3 행렬을 정의한 다음 함께 곱합니다.

예제를 실행하면 먼저 두 부모 행렬이 인쇄된 다음 이를 아다마르 곱과 곱한 결과가 인쇄됩니다.

1
2
3
4
5
6
7
8
[[1 2 3]
 [4 5 6]]
 
[[1 2 3]
 [4 5 6]]
 
[[ 1  4  9]
 [16 25 36]]

매트릭스 분할

한 행렬을 차원이 같은 다른 행렬로 나눌 수 있습니다.

1
C = A / B

결과 행렬의 스칼라 요소는 각 행렬의 요소 분할로 계산됩니다.

1
2
3
         a11 / b11, a12 / b12
A / B = (a21 / b21, a22 / b22)
         a31 / b31, a32 / b32

또는 다른 방법으로 :

1
2
3
4
5
6
C[0,0] = A[0,0] / B[0,0]
C[1,0] = A[1,0] / B[1,0]
C[2,0] = A[2,0] / B[2,0]
C[0,1] = A[0,1] / B[0,1]
C[1,1] = A[1,1] / B[1,1]
C[2,1] = A[2,1] / B[2,1]

두 개의 NumPy 배열에서 직접 나누기 연산자를 사용하여 파이썬에서 이것을 구현할 수 있습니다.

1
2
3
4
5
6
7
8
# divide matrices
from numpy import array
A = array([[1, 2, 3], [4, 5, 6]])
print(A)
B = array([[1, 2, 3], [4, 5, 6]])
print(B)
C = A / B
print(C)

이 예제에서는 먼저 두 개의 2×3 행렬을 정의한 다음 첫 번째 행렬과 두 번째 행렬을 나눕니다.

예제를 실행하면 먼저 두 부모 행렬이 인쇄된 다음 첫 번째 행렬이 두 번째 행렬로 나뉩니다.

1
2
3
4
5
6
7
8
[[1 2 3]
 [4 5 6]]
 
[[1 2 3]
 [4 5 6]]
 
[[ 1.  1.  1.]
 [ 1.  1.  1.]]

행렬-행렬 곱셈(내적)

행렬 내적이라고도 하는 행렬 곱셈은 이전 연산보다 복잡하며 모든 행렬을 곱할 수 없는 규칙이 필요합니다.

1
C = A * B

또는

1
C = AB

행렬 곱셈에 대한 규칙은 다음과 같습니다.

첫 번째 행렬(A)의 열 수(n)는 두 번째 행렬(B)의 행 수(m)와 같아야 합니다.

예를 들어, 행렬 A의 차원은 m행과 n열이고 행렬 B는 차원 n과 k입니다. A와 n 행 b의 n 열은 동일합니다. 결과는 m개의 행과 k개의 열이 있는 새 행렬입니다.

1
C(m,k) = A(m,n) * B(n,k)

이 규칙은 체인의 한 행렬에 있는 열 수가 체인에 있는 다음 행렬의 행 수와 일치해야 하는 행렬 곱셈 체인에 적용됩니다.

행렬과 관련된 가장 중요한 연산 중 하나는 두 행렬의 곱셈입니다. 행렬 A와 B의 행렬 곱은 세 번째 행렬 C입니다. 이 제품을 정의하려면 A에 B에 행이 있는 것과 동일한 수의 열이 있어야 합니다. A가 m × n 모양이고 B가 n × p 모양이면 C는 m × p 모양입니다.

— 34페이지, 딥러닝, 2016.

행렬 곱셈에 대한 직관은 행렬 A의 각 행과 행렬 B의 각 열 사이의 내적을 계산한다는 것입니다. 예를 들어 A 열의 행을 단계별로 실행하고 B의 열 1을 곱하여 C의 열 1에 스칼라 값을 제공 할 수 있습니다.

이는 다음 이미지를 통해 명확해집니다.

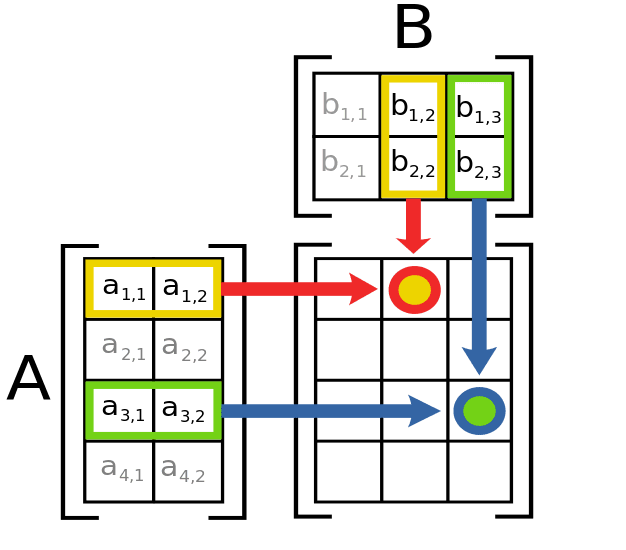
Wikipedia에서 가져온 행렬 곱셈 묘사, 일부 권리 보유.

아래에서는 행렬 표기법을 사용한 행렬 곱셈에 대해 설명합니다.

1
2
3
4
5
6
7
8
9
10
     a11, a12
A = (a21, a22)
     a31, a32
 
     b11, b12
B = (b21, b22)
 
     a11 * b11 + a12 * b21, a11 * b12 + a12 * b22
C = (a21 * b11 + a22 * b21, a21 * b12 + a22 * b22)
     a31 * b11 + a32 * b21, a31 * b12 + a32 * b22

이것은 곱셈 기호를 다음과 같이 제거하여 단순화 할 수 있습니다.

1
2
3
     a11b11 + a12b21, a11b12 + a12b22
C = (a21b11 + a22b21, a21b12 + a22b22)
     a31b11 + a32b21, a31b12 + a32b22

배열 표기법을 사용하여 행렬 곱셈 연산을 설명 할 수 있습니다.

1
2
3
4
5
6
C[0,0] = A[0,0] * B[0,0] + A[0,1] * B[1,0]
C[1,0] = A[1,0] * B[0,0] + A[1,1] * B[1,0]
C[2,0] = A[2,0] * B[0,0] + A[2,1] * B[1,0]
C[0,1] = A[0,0] * B[0,1] + A[0,1] * B[1,1]
C[1,1] = A[1,0] * B[0,1] + A[1,1] * B[1,1]
C[2,1] = A[2,0] * B[0,1] + A[2,1] * B[1,1]

행렬 곱셈 연산은 dot() 함수를 사용하여 NumPy에서 구현할 수 있습니다.

1
2
3
4
5
6
7
8
# matrix dot product
from numpy import array
A = array([[1, 2], [3, 4], [5, 6]])
print(A)
B = array([[1, 2], [3, 4]])
print(B)
C = A.dot(B)
print(C)

이 예제에서는 먼저 두 개의 2×3 행렬을 정의한 다음 해당 내적을 계산합니다.

예제를 실행하면 먼저 두 부모 행렬이 인쇄된 다음 내적의 결과가 인쇄됩니다.

1
2
3
4
5
6
7
8
9
10
[[1 2]
 [3 4]
 [5 6]]
 
[[1 2]
 [3 4]]
 
[[ 7 10]
 [15 22]
 [23 34]]

행렬-벡터 곱셈

행렬과 벡터는 행렬 곱셈 규칙이 준수되는 한 함께 곱할 수 있습니다.

특히, 행렬의 열 개수는 벡터의 항목 개수와 같아야 합니다. 행렬 곱셈과 마찬가지로 점 표기법을 사용하여 연산을 작성할 수 있습니다. 벡터에는 열이 하나만 있기 때문에 결과는 항상 벡터입니다.

1
c = A . v

또는 컴팩트 한 형태의 점이 없습니다.

1
c = Av

결과는 부모 행렬과 행 개수가 같은 벡터입니다.

1
2
3
4
5
6
7
8
9
10
     a11, a12
A = (a21, a22)
     a31, a32
 
     v1
v = (v2)
 
     a11 * v1 + a12 * v2
c = (a21 * v1 + a22 * v2)
     a31 * v1 + a32 * v2

또는 더 컴팩트하게.

1
2
3
     a11v1 + a12v2
c = (a21v1 + a22v2)
     a31v1 + a32v2

행렬-벡터 곱셈은 dot() 함수 또는 @ 연산자(파이썬 버전 3.5 이후)를 사용하여 NumPy에서 구현할 수 있습니다.

1
2
3
4
5
6
7
8
9
10
# matrix-vector multiplication
from numpy import array
A = array([[1, 2], [3, 4], [5, 6]])
print(A)
B = array([0.5, 0.5])
print(B)
C = A.dot(B)
print(C)
D = A @ B
print(D)

이 예제에서는 먼저 3×2 행렬과 2 요소 벡터를 정의한 다음 함께 곱합니다.

예제를 실행하면 먼저 부모 행렬과 벡터가 인쇄된 다음 이들을 곱한 결과가 출력됩니다.

1
2
3
4
5
6
7
8
9
[[1 2]
 [3 4]
 [5 6]]
 
[ 0.5  0.5]
 
[ 1.5  3.5  5.5]
 
[ 1.5  3.5  5.5]

행렬-스칼라 곱셈

행렬에 스칼라를 곱할 수 있습니다.

이것은 행렬과 스칼라 사이의 점 표기법을 사용하여 나타낼 수 있습니다.

1
C = A . b

또는 점 표기법이 없습니다.

1
C = Ab

결과는 부모 행렬과 크기가 같은 행렬이며, 행렬의 각 요소에 스칼라 값을 곱합니다.

1
2
3
4
5
6
7
8
9
     a11, a12
A = (a21, a22)
     a31, a32
 
b
 
     a11 * b, a12 * b
C = (a21 * b, a22 * b)
     a31 * b, a32 * b

또는

1
2
3
     a11b, a12b
C = (a21b, a22b)
     a31b, a32b

배열 표기법으로 이것을 나타낼 수도 있습니다.

1
2
3
4
5
6
C[0,0] = A[0,0] * b
C[1,0] = A[1,0] * b
C[2,0] = A[2,0] * b
C[0,1] = A[0,1] * b
C[1,1] = A[1,1] * b
C[2,1] = A[2,1] * b

이것은 곱셈 연산자를 사용하여 NumPy에서 직접 구현할 수 있습니다.

1
2
3
4
5
6
7
8
# matrix-scalar multiplication
from numpy import array
A = array([[1, 2], [3, 4], [5, 6]])
print(A)
b = 0.5
print(b)
C = A * b
print(C)

이 예제에서는 먼저 2×3 행렬과 스칼라를 정의한 다음 함께 곱합니다.

예제를 실행하면 먼저 부모 행렬과 스칼라가 인쇄된 다음 두 행렬을 곱한 결과가 출력됩니다.

1
2
3
4
5
6
7
8
9
[[1 2]
 [3 4]
 [5 6]]
 
0.5
 
[[ 0.5  1. ]
 [ 1.5  2. ]
 [ 2.5  3. ]]

확장

이 섹션에는 탐색할 수 있는 자습서를 확장하기 위한 몇 가지 아이디어가 나열되어 있습니다.

자체 데이터를 사용하여 각 작업을 사용하여 5 개의 예제를 만듭니다.
목록 목록으로 정의된 행렬에 대해 각 행렬 연산을 수동으로 구현합니다.
머신러닝 문서를 검색하고 사용 중인 각 작업의 예제 1개를 찾습니다.

이러한 확장 기능을 탐색하면 알고 싶습니다.

더 많은 튜토리얼

행렬에는 여러 가지 유형이 있으며 몇 가지 예는 다음을 참조하십시오.

머신러닝을 위한 선형 대수학의 행렬 유형 소개

행렬은 다양한 연산에 사용되며, 몇 가지 예는 다음을 참조하십시오.

머신러닝을 위한 매트릭스 연산에 대한 짧은 소개

추가 정보

이 섹션에서는 더 자세히 알아보려는 경우 주제에 대한 더 많은 리소스를 제공합니다.

책

섹션 2.3, 행렬 연산. 선형 대수학에 대한 좋은 가이드, 2017.
섹션 3.3, 행렬 곱셈. 선형 대수학에 대한 좋은 가이드, 2017.
섹션 1.3 행렬, 선형 대수학 입문, 제 5 판, 2016.
섹션 2.4 행렬 연산 규칙, 선형 대수학 입문, 제 5 판, 2016.
섹션 2.1 스칼라, 벡터, 행렬 및 텐서, 딥러닝, 2016.
섹션 2.2 행렬과 벡터 곱하기, 딥러닝, 2016.

API

기사

요약

이 튜토리얼에서는 선형 대수학의 행렬과 Python에서 행렬을 조작하는 방법을 발견했습니다.

특히 다음 내용을 배웠습니다.

행렬이란 무엇이며 NumPy를 사용하여 파이썬에서 행렬을 정의하는 방법.
덧셈, 뺄셈, 아다마르 곱과 같은 요소별 연산을 수행하는 방법.
행렬을 곱하는 방법과 연산 이면의 직관.

Tags:

Machine learning,Matrices