머신러닝에 대한 KL 발산을 계산하는 방법

29 11월

머신러닝에 대한 KL 발산을 계산하는 방법

주어진 확률 변수에 대한 확률 분포 간의 차이를 정량화 하는 것이 종종 바람직합니다.

이것은 실제 확률 분포와 관찰 된 확률 분포의 차이를 계산하는 데 관심이 있을 수 있는 머신러닝에서 자주 발생합니다.

이것은 Kullback-Leibler Divergence (KL 발산) 또는 상대 엔트로피와 같은 정보 이론의 기술과 KL 발산의 정규화 되고 대칭적인 버전을 제공하는 Jensen-Shannon Divergence를 사용하여 달성 할 수 있습니다. 이러한 점수 매기기 방법은 모델링 전에 특징 선택을 위한 상호 정보 및 다양한 분류기 모델에 대한 손실 함수로 사용되는 교차 엔트로피와 같이 널리 사용되는 다른 방법의 계산에서 바로 가기로 사용할 수 있습니다.

이 게시물에서는 확률 분포 간의 차이를 계산하는 방법을 알아봅니다.

이 게시물을 읽은 후 다음을 알게 될 것입니다.

통계적 거리는 확률 변수에 대한 다른 확률 분포와 같은 통계 객체 간의 차이를 계산하는 일반적인 아이디어입니다.
Kullback-Leibler 발산은 한 확률 분포와 다른 확률 분포의 차이를 측정하는 점수를 계산합니다.
Jensen-Shannon 발산은 KL 발산을 확장하여 한 확률 분포의 대칭 점수 및 거리 측도를 계산합니다.

개요

이 자습서는 다음과 같이 세 부분으로 나뉩니다.

통계적 거리
쿨백-라이블러 분기
젠슨-섀넌 분기

통계적 거리

두 확률 분포를 비교해야 하는 경우가 많습니다.

특히, 변수에 대해 단일 확률 변수와 두 개의 다른 확률 분포(예: 실제 분포 및 해당 분포의 근사치)가 있을 수 있습니다.

이와 같은 상황에서는 분포 간의 차이를 수량화하는 것이 유용할 수 있습니다. 일반적으로 이를 두 통계 대상(예: 확률 분포) 사이의 통계적 거리를 계산하는 문제라고 합니다.

한 가지 방법은 두 분포 사이의 거리 측정값을 계산하는 것입니다. 측정값을 해석하기 어려울 수도 있습니다.

대신 두 확률 분포 간의 차이를 계산하는 것이 더 일반적입니다. 발산은 측정값과 비슷하지만 대칭이 아닙니다. 즉, 발산은 한 분포가 다른 분포와 어떻게 다른지에 대한 점수이며, 분포 P와 Q에 대한 발산을 계산하면 Q 및 P와 다른 점수를 얻을 수 있습니다.

발산 점수는 정보 이론 및 보다 일반적으로 머신러닝에서 다양한 계산을 위한 중요한 기초입니다. 예를 들어, 분류 모델의 손실 함수로 사용되는 상호 정보(정보 획득) 및 교차 엔트로피와 같은 점수를 계산하기 위한 바로 가기를 제공합니다.

발산 점수는 생성적 적대 신경망(GAN) 모델을 최적화할 때 목표 확률 분포를 근사화하는 것과 같은 복잡한 모델링 문제를 이해하기 위한 도구로도 직접 사용됩니다.

정보 이론에서 일반적으로 사용되는 두 가지 발산 점수는 Kullback-Leibler Divergence와 Jensen-Shannon Divergence입니다.

다음 섹션에서 이 두 점수를 자세히 살펴보겠습니다.

쿨백-라이블러 분기

Kullback-Leibler발산 점수 또는 KL 발산 점수는 한 확률 분포가 다른 확률 분포와 얼마나 다른지를 정량화합니다.

두 분포 Q와 P 사이의 KL 발산은 종종 다음 표기법을 사용하여 명시됩니다.

KL(P || Q)

여기서 “||” 연산자는 Q에서 “발산” 또는 Ps 발산을 나타냅니다.

KL 발산은 P의 각 사건 확률의 음의 합에 P의 사건 확률에 대한 Q의 사건 확률 로그를 곱한 값으로 계산할 수 있습니다.

KL(P || Q) = – X P(x) * log(Q(x) / P(x))의 합계 x

합계 내의 값은 주어진 사건에 대한 발산입니다.

이것은 P의 각 사건 확률의 양수 합에 Q의 사건 확률에 대한 P의 사건 확률 로그를 곱한 것과 같습니다 (예 : 분수의 항이 뒤집힙니다). 이것은 실제로 사용되는 더 일반적인 구현입니다.

KL(P || Q) = X P(x) * 로그(P(x) / Q(x))의 합계 x

KL 발산 점수에 대한 직관은 P의 사건에 대한 확률이 크지만 Q에서 동일한 사건에 대한 확률이 작을 때 큰 발산이 있다는 것입니다. P로부터의 확률이 작고 Q로부터의 확률이 클 때, 또한 큰 차이가 있지만 첫 번째 경우만큼 크지는 않습니다.

이산 확률 분포와 연속 확률 분포 간의 발산을 측정하는 데 사용할 수 있으며, 후자의 경우 이산 사건의 확률의 합 대신 사건의 적분이 계산됩니다.

두 확률 분포 p와 q의 비유사성을 측정하는 한 가지 방법은 쿨백-라이블러 발산(KL 발산) 또는 상대 엔트로피로 알려져 있습니다.

— 페이지 57, 머신러닝: 확률론적 관점, 2012.

로그는 단위를 “비트“로 제공하는 기본 2이거나 “nats“의 단위를 제공하는 자연 로그 base-e일 수 있습니다. 점수가 0이면 두 분포가 동일하다는 것을 나타내고, 그렇지 않으면 점수가 양수임을 나타냅니다.

중요한 것은 KL 발산 점수가 다음과 같이 대칭이 아니라는 것입니다.

KL(P || Q) != KL(Q || P)

솔로몬 쿨백 (Solomon Kullback)과 리처드 라이블러 (Richard Leibler) 방법의 두 저자의 이름을 따서 명명되었으며 때로는 “상대 엔트로피“라고도합니다.

이것은 분포 p(x)와 q(x) 사이의 상대 엔트로피 또는 쿨백-라이블러 발산 또는 KL 발산으로 알려져 있습니다.

— 페이지 55, 패턴 인식 및 머신러닝, 2006.

알 수 없는 확률 분포를 근사하려고 하면 데이터의 목표 확률 분포는 P이고 Q는 분포의 근사치입니다.

이 경우 KL 발산은 랜덤 변수에서 이벤트를 나타내는 데 필요한 추가 비트 수(즉, 밑이 2인 로그로 계산)를 요약합니다. 근사치가 좋을수록 추가 정보가 덜 필요합니다.

… KL 발산은 데이터를 인코딩하는 데 필요한 평균 추가 비트 수로, 실제 분포 p 대신 분포 q를 사용하여 데이터를 인코딩했기 때문입니다.

— 페이지 58, 머신러닝: 확률론적 관점, 2012.

작업된 예를 사용하여 KL 발산을 만들 수 있습니다.

세 개의 사건이 서로 다른 색으로 있는 랜덤 변수를 고려합니다. 이 변수에 대해 두 가지 다른 확률 분포가 있을 수 있습니다. 예를 들어:

1
2
3
4
5
...
# define distributions
events = [‘red’, ‘green’, ‘blue’]
p = [0.10, 0.40, 0.50]
q = [0.80, 0.15, 0.05]

이러한 확률의 막대 차트를 플로팅하여 확률 히스토그램으로 직접 비교할 수 있습니다.

전체 예제는 다음과 같습니다.

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
# plot of distributions
from matplotlib import pyplot
# define distributions
events = [‘red’, ‘green’, ‘blue’]
p = [0.10, 0.40, 0.50]
q = [0.80, 0.15, 0.05]
print(‘P=%.3f Q=%.3f’ % (sum(p), sum(q)))
# plot first distribution
pyplot.subplot(2,1,1)
pyplot.bar(events, p)
# plot second distribution
pyplot.subplot(2,1,2)
pyplot.bar(events, q)
# show the plot
pyplot.show()

예제를 실행하면 각 확률 분포에 대한 히스토그램이 생성되어 각 사건의 확률을 직접 비교할 수 있습니다.

실제로 분포가 다르다는 것을 알 수 있습니다.

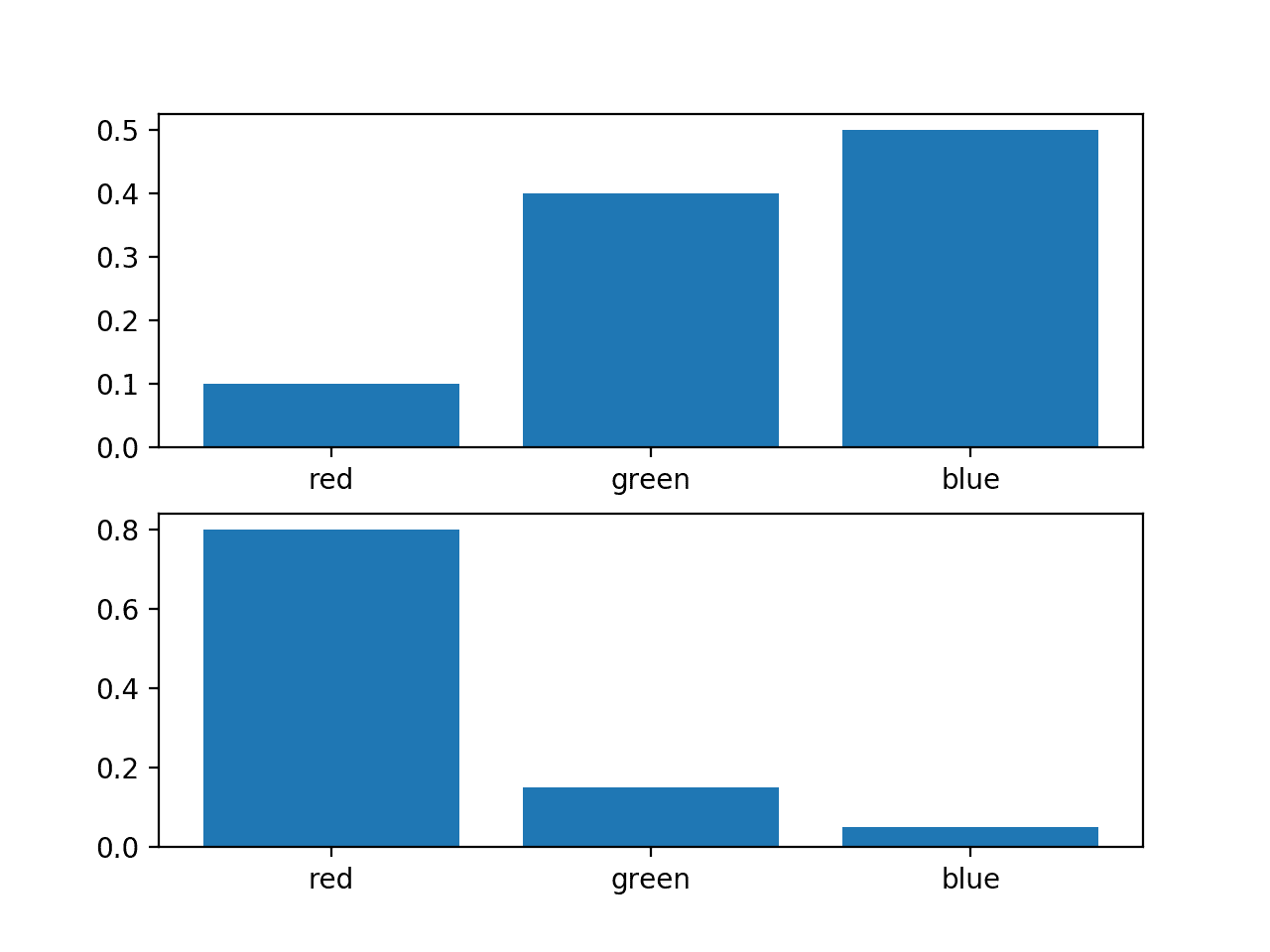
동일한 랜덤 변수에 대한 두 개의 서로 다른 확률 분포의 히스토그램

다음으로 두 분포 간의 KL 발산을 계산하는 함수를 개발할 수 있습니다.

log base-2를 사용하여 결과에 비트 단위의 단위가 있는지 확인합니다.

1
2
3
# calculate the kl divergence
def kl_divergence(p, q):
	return sum(p[i] * log2(p[i]/q[i]) for i in range(len(p)))

그런 다음이 함수를 사용하여 Q에서 P의 KL 발산과 P에서 그 반대의 Q를 계산할 수 있습니다.

1
2
3
4
5
6
# calculate (P || Q)
kl_pq = kl_divergence(p, q)
print(‘KL(P || Q): %.3f bits’ % kl_pq)
# calculate (Q || P)
kl_qp = kl_divergence(q, p)
print(‘KL(Q || P): %.3f bits’ % kl_qp)

이 모든 것을 함께 묶어 전체 예제가 아래에 나열되어 있습니다.

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
# example of calculating the kl divergence between two mass functions
from math import log2
 
# calculate the kl divergence
def kl_divergence(p, q):
	return sum(p[i] * log2(p[i]/q[i]) for i in range(len(p)))
 
# define distributions
p = [0.10, 0.40, 0.50]
q = [0.80, 0.15, 0.05]
# calculate (P || Q)
kl_pq = kl_divergence(p, q)
print(‘KL(P || Q): %.3f bits’ % kl_pq)
# calculate (Q || P)
kl_qp = kl_divergence(q, p)
print(‘KL(Q || P): %.3f bits’ % kl_qp)

예제를 실행하면 먼저 Q에서 P의 발산이 2비트 미만으로 계산된 다음 P에서 Q의 발산이 2비트를 약간 넘는 것으로 계산됩니다.

Q가 작을 때 P가 큰 확률을 갖는다고 가정하면 P가 큰 확률을 가질 때 Q가 더 작은 확률을 갖기 때문에 P에서 Q보다 발산이 적습니다. 이 두 번째 경우에는 더 많은 차이가 있습니다.

1
2
KL(P || Q): 1.927 bits
KL(Q || P): 2.022 bits

log2()를 자연 로그log() 함수로 변경하면 결과는 다음과 같이 nats에 표시됩니다.

1
2
# KL(P || Q): 1.336 nats
# KL(Q || P): 1.401 nats

SciPy 라이브러리는 KL 발산을 계산하기 위한 kl_div() 함수를 제공하지만 여기에 정의된 정의는 다릅니다. 또한 여기서 KL 발산의 정의와 일치하는 상대 엔트로피를 계산하기 위한 rel_entr() 함수를 제공합니다. “상대 엔트로피“가 종종 “KL 발산“의 동의어로 사용되기 때문에 이것은 이상합니다.

그럼에도 불구하고 rel_entr() SciPy 함수를 사용하여 KL 발산을 계산하고 수동 계산이 올바른지 확인할 수 있습니다.

rel_entr()함수는 각 확률 분포의 모든 사건에 대한 확률 목록을 인수로 사용하고 각 사건에 대한 분기 목록을 반환합니다. 이를 합산하여 KL 발산을 제공할 수 있습니다. 계산은 log base-2 대신 자연 로그를 사용하므로 단위는 비트 대신 nats에 있습니다.

ScPy를 사용하여 KL(P || Q) 및 KL(Q || P) 위에 사용된 동일한 확률 분포에 대해 다음과 같습니다.

1
2
3
4
5
6
7
8
9
10
11
# example of calculating the kl divergence (relative entropy) with scipy
from scipy.special import rel_entr
# define distributions
p = [0.10, 0.40, 0.50]
q = [0.80, 0.15, 0.05]
# calculate (P || Q)
kl_pq = rel_entr(p, q)
print(‘KL(P || Q): %.3f nats’ % sum(kl_pq))
# calculate (Q || P)
kl_qp = rel_entr(q, p)
print(‘KL(Q || P): %.3f nats’ % sum(kl_qp))

예제를 실행하면 계산된 발산이 KL(P || Q) 및 KL(Q || P) 각각.

1
2
KL(P || Q): 1.336 nats
KL(Q || P): 1.401 nats

젠슨-섀넌 분기

Jensen-Shannon 발산 또는 줄여서 JS 발산은 두 확률 분포 간의 차이(또는 유사성)를 정량화하는 또 다른 방법입니다.

KL 발산을 사용하여 대칭인 정규화된 점수를 계산합니다. 이것은 Q에서 P의 발산이 P에서 Q와 동일하거나 공식적으로 명시되었음을 의미합니다.

JS(P || Q) == JS(Q || P)

JS 발산은 다음과 같이 계산할 수 있습니다.

JS(P || Q) = 1/2 * KL(P || M) + 1/2 * KL(Q || M)

여기서 M은 다음과 같이 계산됩니다.

M = 1/2 * (P + Q)

그리고 KL()은 이전 섹션에서 설명한 KL 발산으로 계산됩니다.

밑-2 로그를 사용할 때 0(동일)과 1(최대로 다름) 사이의 점수로 KL 발산의 평활화되고 정규화된 버전을 제공하므로 측정값으로 더 유용합니다.

점수의 제곱근은 Jensen-Shannon 거리 또는 줄여서 JS 거리라고하는 양을 제공합니다.

작업된 예를 통해 JS 분기를 구체적으로 만들 수 있습니다.

먼저 이전 섹션에서 준비한 kl_divergence()함수를 사용하는 JS 발산을 계산하는 함수를 정의할 수 있습니다.

1
2
3
4
5
6
7
8
# calculate the kl divergence
def kl_divergence(p, q):
	return sum(p[i] * log2(p[i]/q[i]) for i in range(len(p)))
 
# calculate the js divergence
def js_divergence(p, q):
	m = 0.5 * (p + q)
	return 0.5 * kl_divergence(p, m) + 0.5 * kl_divergence(q, m)

그런 다음 이전 섹션에서 사용된 것과 동일한 확률 분포를 사용하여 이 함수를 테스트할 수 있습니다.

먼저 분포에 대한 JS 발산 점수를 계산 한 다음 점수의 제곱근을 계산하여 분포 사이의 JS 거리를 제공합니다. 예를 들어:

1
2
3
4
5
...
# calculate JS(P || Q)
js_pq = js_divergence(p, q)
print(‘JS(P || Q) divergence: %.3f bits’ % js_pq)
print(‘JS(P || Q) distance: %.3f’ % sqrt(js_pq))

그런 다음 반대의 경우에 대해 이를 반복하여 발산이 KL 발산과 달리 대칭임을 나타낼 수 있습니다.

1
2
3
4
5
...
# calculate JS(Q || P)
js_qp = js_divergence(q, p)
print(‘JS(Q || P) divergence: %.3f bits’ % js_qp)
print(‘JS(Q || P) distance: %.3f’ % sqrt(js_qp))

이를 함께 묶어 JS 발산 및 JS 거리를 계산하는 전체 예가 아래에 나열되어 있습니다.

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
# example of calculating the js divergence between two mass functions
from math import log2
from math import sqrt
from numpy import asarray
 
# calculate the kl divergence
def kl_divergence(p, q):
	return sum(p[i] * log2(p[i]/q[i]) for i in range(len(p)))
 
# calculate the js divergence
def js_divergence(p, q):
	m = 0.5 * (p + q)
	return 0.5 * kl_divergence(p, m) + 0.5 * kl_divergence(q, m)
 
# define distributions
p = asarray([0.10, 0.40, 0.50])
q = asarray([0.80, 0.15, 0.05])
# calculate JS(P || Q)
js_pq = js_divergence(p, q)
print(‘JS(P || Q) divergence: %.3f bits’ % js_pq)
print(‘JS(P || Q) distance: %.3f’ % sqrt(js_pq))
# calculate JS(Q || P)
js_qp = js_divergence(q, p)
print(‘JS(Q || P) divergence: %.3f bits’ % js_qp)
print(‘JS(Q || P) distance: %.3f’ % sqrt(js_qp))

예제를 실행하면 분포 간의 JS 발산이 약 0.4비트이고 거리가 약 0.6임을 알 수 있습니다.

계산이 대칭임을 알 수 있으며 JS(P || Q) 및 JS(Q || P).

1
2
3
4
JS(P || Q) divergence: 0.420 bits
JS(P || Q) distance: 0.648
JS(Q || P) divergence: 0.420 bits
JS(Q || P) distance: 0.648

SciPy 라이브러리는 jensenshannon() 함수를 통해 JS 거리의 구현을 제공합니다.

각 확률 분포의 모든 이벤트에 대한 확률 배열을 인수로 사용하고 발산 점수가 아닌 JS 거리 점수를 반환합니다. 이 기능을 사용하여 JS 거리의 수동 계산을 확인할 수 있습니다.

전체 예제는 다음과 같습니다.

1
2
3
4
5
6
7
8
9
10
11
12
# calculate the jensen-shannon distance metric
from scipy.spatial.distance import jensenshannon
from numpy import asarray
# define distributions
p = asarray([0.10, 0.40, 0.50])
q = asarray([0.80, 0.15, 0.05])
# calculate JS(P || Q)
js_pq = jensenshannon(p, q, base=2)
print(‘JS(P || Q) Distance: %.3f’ % js_pq)
# calculate JS(Q || P)
js_qp = jensenshannon(q, p, base=2)
print(‘JS(Q || P) Distance: %.3f’ % js_qp)

예제를 실행하면 거리 점수가 수동 계산인 0.648과 일치하고 거리 계산이 예상대로 대칭임을 확인할 수 있습니다.

1
2
JS(P || Q) Distance: 0.648
JS(Q || P) Distance: 0.648

추가 정보

이 섹션에서는 더 자세히 알아보려는 경우 주제에 대한 더 많은 리소스를 제공합니다.