정규 요약 통계 계산에 대한 짧은 소개
데이터 샘플은 도메인에서 생성되거나 프로세스에서 생성될 수 있는 모든 가능한 관측치의 광범위한 모집단의 스냅샷입니다.
흥미롭게도 많은 관측치는 정규 분포 또는 더 공식적으로 가우스 분포라고 하는 일반적인 패턴이나 분포에 적합합니다. 가우스 분포에 대해 많이 알려져 있으며, 따라서 가우스 데이터와 함께 사용할 수있는 통계 및 통계 방법의 전체 하위 필드가 있습니다.
이 자습서에서는 가우스 분포, 가우스 분포를 식별하는 방법 및 이 분포에서 추출한 데이터의 주요 요약 통계를 계산하는 방법을 알아봅니다.
이 자습서를 완료하면 다음을 알 수 있습니다.
- 가우스 분포는 적용된 머신러닝 중에 본 많은 관찰을 포함하여 많은 관찰을 설명합니다.
- 분포의 중심 경향이 가장 가능성이 높은 관측치이며 데이터 표본에서 평균 또는 중위수로 추정할 수 있습니다.
- 분산은 분포의 평균으로부터의 평균 편차이며 데이터 표본에서 분산 및 표준 편차로 추정할 수 있습니다.
튜토리얼 개요
이 튜토리얼은 다음과 같이 6 부분으로 나뉩니다.
- 가우스 분포
- 표본 대 모집단
- 테스트 데이터 세트
- 중심 경향
- 분산
- 가우스 설명
가우스 분포
데이터 분포는 히스토그램과 같이 그래프로 표시할 때의 모양을 나타냅니다.
가장 일반적으로 볼 수 있고 따라서 잘 알려진 연속 값 분포는 종형 곡선입니다. 많은 데이터가 속하는 분포이기 때문에 “정규” 분포라고 합니다. 가우스 분포라고도 하며, 보다 공식적으로는 칼 프리드리히 가우스 (Carl Friedrich Gauss)의 이름을 따서 명명되었습니다.
따라서 정규 분포 또는 가우스 데이터에 대한 참조는 상호 교환 가능하며 둘 다 동일한 것을 나타냅니다 : 데이터가 가우스 분포처럼 보입니다.
가우스 분포를 갖는 관측치의 몇 가지 예는 다음과 같습니다.
- 사람들의 키.
- IQ 점수.
- 체온.
정규 분포를 살펴보겠습니다. 다음은 이상적인 가우스 분포를 생성하고 플로팅하는 코드입니다.
1 2 3 4 5 6 7 8 9 10 11 | # generate and plot an idealized gaussian from numpy import arange from matplotlib import pyplot from scipy.stats import norm # x-axis for the plot x_axis = arange(–3, 3, 0.001) # y-axis as the gaussian y_axis = norm.pdf(x_axis, 0, 1) # plot data pyplot.plot(x_axis, y_axis) pyplot.show() |
예제를 실행하면 이상적인 가우스 분포의 플롯이 생성됩니다.
x축은 관측치이고 y축은 각 관측치의 빈도입니다. 이 경우 0.0 부근의 관측치가 가장 일반적이며 -3.0과 3.0 부근의 관측치는 드물거나 가능성이 낮습니다.
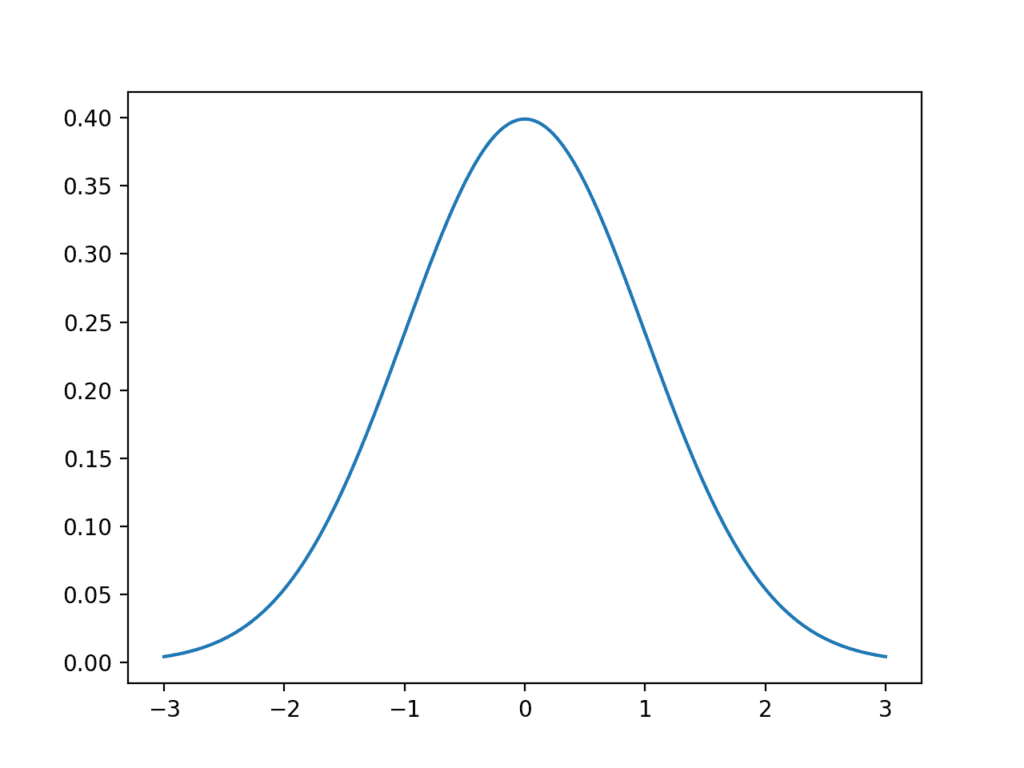
가우스 분포의 선 그림
데이터가 가우스이거나 통계를 계산하기 위해 가우스 분포를 가정할 때 유용합니다. 이것은 가우스 분포가 매우 잘 이해되기 때문입니다. 통계 분야의 많은 부분이 이 분포 방법을 사용하고 있습니다.
고맙게도 머신러닝에서 작업하는 많은 데이터는 모델을 맞추는 데 사용할 수 있는 입력 데이터와 같은 가우스 분포를 다양한 학습 데이터 샘플에 대한 모델의 반복 평가에 적합한 경우가 많습니다.
모든 데이터가 가우스인 것은 아니며, 데이터의 히스토그램 플롯을 검토하거나 통계 테스트를 사용하여 탐색을 수행하는 것이 중요할 때가 있습니다. 가우스 분포에 적합하지 않은 관측치의 몇 가지 예는 다음과 같습니다.
- 사람들의 소득.
- 도시의 인구.
- 책 판매.
표본 대 모집단
알 수 없는 프로세스에 의해 데이터가 생성된다고 생각할 수 있습니다.
수집하는 데이터를 데이터 샘플이라고 하는 반면 수집할 수 있는 모든 가능한 데이터를 모집단이라고 합니다.
- 데이터 샘플: 그룹의 관측치의 하위 집합입니다.
- 데이터 모집단: 그룹에서 가능한 모든 관측치입니다.
이는 표본과 모집단에 대해 서로 다른 통계 방법이 사용되고 응용 머신러닝에서 종종 데이터 표본으로 작업하기 때문에 중요한 차이점입니다. 머신러닝에서 데이터에 대해 말할 때 “인구“라는 단어를 읽거나 사용하면 통계적 방법과 관련하여 샘플을 의미할 가능성이 큽니다.
머신러닝에서 접하게 될 데이터 샘플의 두 가지 예는 다음과 같습니다.
- 학습 및 테스트 데이터 세트입니다.
- 모델의 성능 점수입니다.
통계적 방법을 사용할 때 표본의 관측치만 사용하여 모집단에 대한 주장을 하려는 경우가 많습니다.
이에 대한 두 가지 명확한 예는 다음과 같습니다.
- 훈련 표본은 유용한 모형을 적합시킬 수 있도록 관측치 모집단을 대표해야 합니다.
- 검정 표본은 모형 기술에 대한 편향되지 않은 평가를 개발할 수 있도록 관측치 모집단을 대표해야 합니다.
우리는 표본으로 작업하고 모집단에 대해 클레임하기 때문에 항상 약간의 불확실성이 있음을 의미하며 이 불확실성을 이해하고 보고하는 것이 중요합니다.
테스트 데이터 세트
가우스 분포를 사용하는 데이터에 대한 몇 가지 중요한 요약 통계량을 살펴보기 전에 먼저 작업할 수 있는 데이터 샘플을 생성해 보겠습니다.
randn()NumPy 함수를 사용하여 가우스 분포에서 추출한 난수 샘플을 생성할 수 있습니다.
가우스 분포를 정의하는 두 가지 주요 매개 변수가 있습니다. 평균과 표준 편차입니다. 이러한 매개변수는 알려지지 않은 가우스 분포에서 가져온 데이터가 있을 때 추정하는 핵심 통계이기도 하므로 나중에 자세히 살펴보겠습니다.
randn() 함수는 평균이 0이고 표준 편차가 1 인 가우스 분포에서 추출한 지정된 수의 난수 (예 : 10,000)를 생성합니다. 그런 다음 숫자를 다시 스케일링하여 이 숫자를 선택한 가우스로 스케일링할 수 있습니다.
이는 원하는 평균(예: 50)을 더하고 값에 표준 편차(5)를 곱하여 일관성을 유지할 수 있습니다.
1 | data = 5 * randn(10000) + 50 |
그런 다음 히스토그램을 사용하여 데이터 세트를 플로팅하고 플로팅된 데이터의 예상 모양을 찾을 수 있습니다.
전체 예제는 다음과 같습니다.
1 2 3 4 5 6 7 8 9 10 11 | # generate a sample of random gaussians from numpy.random import seed from numpy.random import randn from matplotlib import pyplot # seed the random number generator seed(1) # generate univariate observations data = 5 * randn(10000) + 50 # histogram of generated data pyplot.hist(data) pyplot.show() |
예제를 실행하면 데이터 집합이 생성되고 히스토그램으로 플로팅됩니다.
데이터에 대한 가우스 모양을 거의 볼 수 있지만 뭉툭합니다. 이것은 중요한 점을 강조합니다.
때로는 데이터가 완벽한 가우스가 아니지만 가우스와 같은 분포를 갖게됩니다. 거의 가우스이며 다른 방식으로 플롯되거나 어떤 방식으로 확장되거나 더 많은 데이터가 수집되면 더 가우스가 될 수 있습니다.
종종 가우스와 같은 데이터로 작업 할 때 가우스로 취급하고 동일한 통계 도구를 모두 사용하여 신뢰할 수있는 결과를 얻을 수 있습니다.
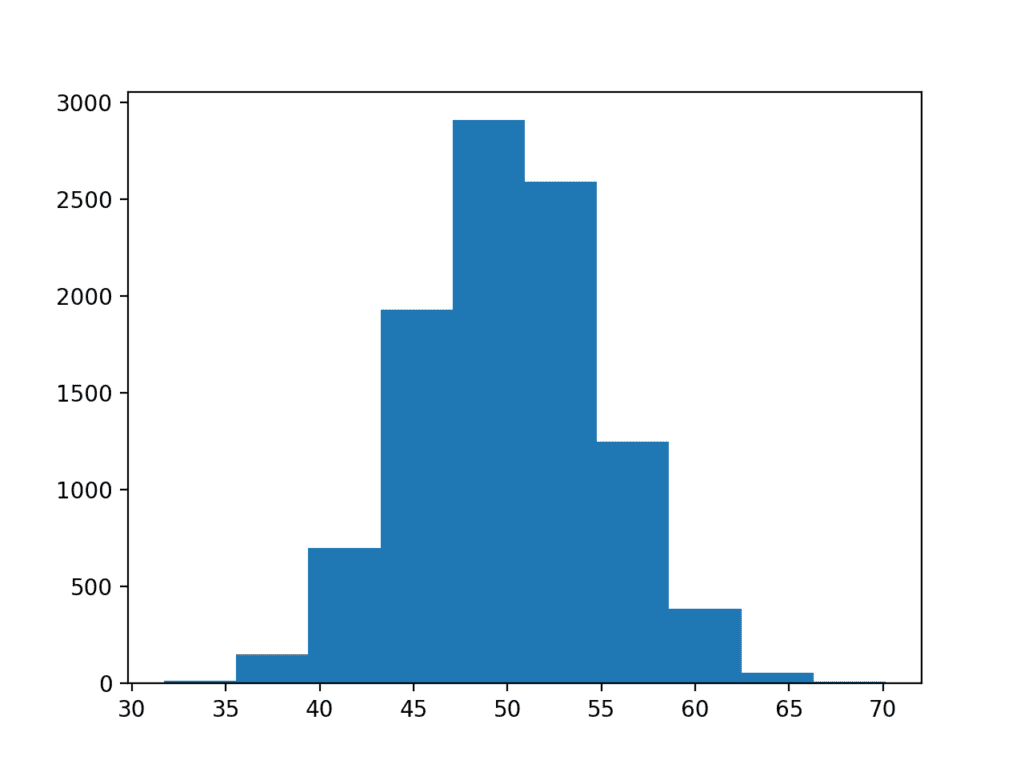
가우스 데이터셋의 히스토그램 플롯
이 데이터 세트의 경우 충분한 데이터가 있으며 플로팅 함수가 데이터를 분할하기 위해 임의의 크기의 버킷을 선택하기 때문에 플롯이 뭉툭합니다. 데이터를 분할하고 기본 가우스 분포를 더 잘 노출하는 보다 세분화 된 방법을 선택할 수 있습니다.
보다 구체화된 플롯으로 업데이트된 예제는 다음과 같습니다.
1 2 3 4 5 6 7 8 9 10 11 | # generate a sample of random gaussians from numpy.random import seed from numpy.random import randn from matplotlib import pyplot # seed the random number generator seed(1) # generate univariate observations data = 5 * randn(10000) + 50 # histogram of generated data pyplot.hist(data, bins=100) pyplot.show() |
예제를 실행하여 데이터의 100 분할을 선택하면 데이터의 가우스 분포를 명확하게 보여주는 플롯을 만드는 것이 훨씬 더 효과적이라는 것을 알 수 있습니다.
데이터 세트는 완벽한 가우스에서 생성되었지만 숫자는 무작위로 선택되었으며 샘플에 대해 10,000개의 관측값만 선택했습니다. 이 제어된 설정에서도 데이터 샘플에 명백한 노이즈가 있음을 알 수 있습니다.
이것은 또 다른 중요한 점을 강조합니다 : 우리는 항상 데이터 샘플에서 약간의 노이즈 또는 제한을 예상해야 합니다. 데이터 샘플에는 순수 기본 분포와 비교하여 항상 오류가 포함됩니다.
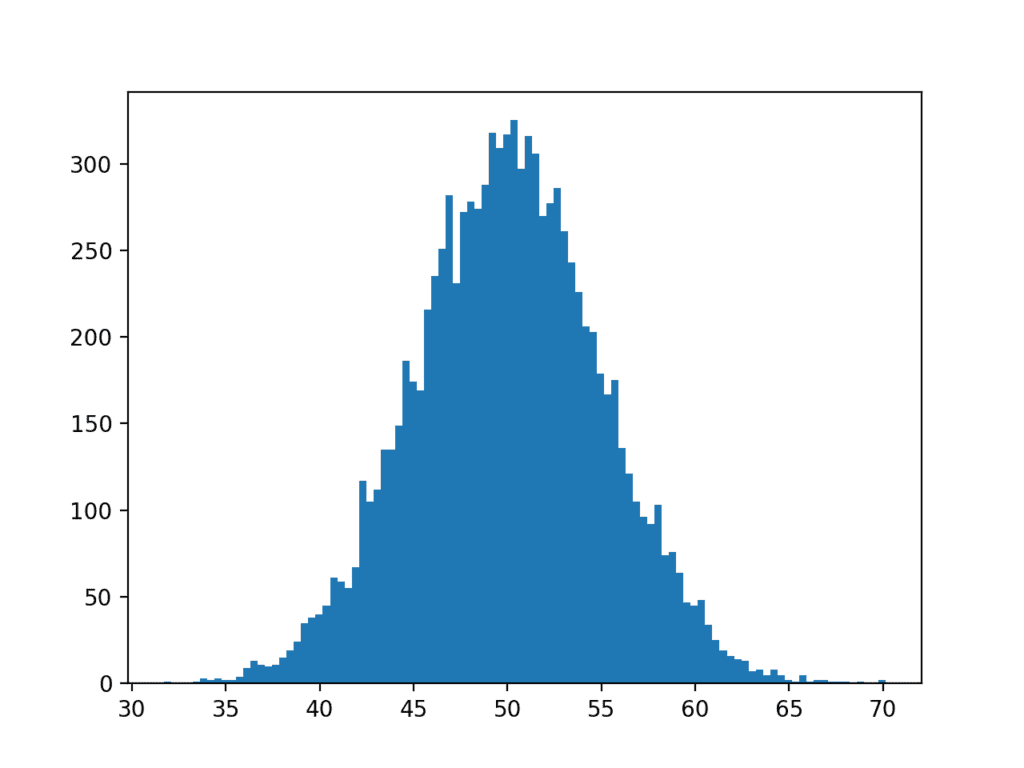
더 많은 Bin이 있는 가우스 데이터셋의 히스토그램 플롯
중심 경향
분포의 중심 경향은 분포의 중간 또는 일반 값을 나타냅니다. 가장 일반적이거나 가장 가능성이 높은 값입니다.
가우스 분포에서 중심 경향은 평균 또는 더 공식적으로 산술 평균이라고 하며 가우스 분포를 정의하는 두 가지 주요 매개 변수 중 하나입니다.
표본의 평균은 관측치의 합을 표본의 총 관측치 수로 나눈 값으로 계산됩니다.
1 | mean = sum(data) / length(data) |
또한 다음과 같이 더 컴팩트한 형식으로 작성됩니다.
1 | mean = 1 / length(data) * sum(data) |
배열에서 mean()NumPy 함수를 사용하여 샘플의 평균을 계산할 수 있습니다.
1 | result = mean(data) |
아래 예제에서는 이전 섹션에서 개발한 테스트 데이터 세트에서 이를 보여 줍니다.
1 2 3 4 5 6 7 8 9 10 11 | # calculate the mean of a sample from numpy.random import seed from numpy.random import randn from numpy import mean # seed the random number generator seed(1) # generate univariate observations data = 5 * randn(10000) + 50 # calculate mean result = mean(data) print(‘Mean: %.3f’ % result) |
예제를 실행하면 표본의 평균이 계산되고 인쇄됩니다.
표본의 산술 평균에 대한 이 계산은 표본이 추출된 모집단의 기본 가우스 분포의 매개변수의 추정치입니다. 추정치로 오류가 포함됩니다.
기본 분포의 실제 평균이 50이라는 것을 알고 있기 때문에 10,000개의 관측치로 구성된 표본의 추정치가 상당히 정확하다는 것을 알 수 있습니다.
1 | Mean: 50.049 |
평균은 특이치 값, 즉 평균에서 멀리 떨어진 희귀 값의 영향을 쉽게 받습니다. 이는 분포 또는 오류의 가장자리에서 합법적으로 드문 관찰 일 수 있습니다.
또한 평균이 오해의 소지가 있습니다. 균일 분포 또는 전력 분포와 같은 다른 분포에 대한 평균을 계산하는 것은 값을 계산할 수 있지만 분포의 진정한 중심 경향보다는 겉보기에 임의적인 기대값을 참조하기 때문에 의미가 없을 수 있습니다.
특이치 또는 비가우스 분포의 경우 계산에 일반적으로 사용되는 대체 중심 경향은 중앙값입니다.
중앙값은 먼저 모든 데이터를 정렬한 다음 표본에서 중간 값을 찾아 계산됩니다. 홀수 개의 관측치가 있는 경우 간단합니다. 관측치 수가 짝수인 경우 중위수는 중간 두 관측치의 평균으로 계산됩니다.
median()NumPy 함수를 호출하여 배열 샘플의 중앙값을 계산할 수 있습니다.
1 | result = median(data) |
아래 예제에서는 테스트 데이터 세트에서 이를 보여 줍니다.
1 2 3 4 5 6 7 8 9 10 11 | # calculate the median of a sample from numpy.random import seed from numpy.random import randn from numpy import median # seed the random number generator seed(1) # generate univariate observations data = 5 * randn(10000) + 50 # calculate median result = median(data) print(‘Median: %.3f’ % result) |
예제를 실행하면 중앙값이 샘플에서 계산되어 인쇄되는 것을 볼 수 있습니다.
결과는 표본이 가우스 분포를 갖기 때문에 평균과 크게 다르지 않습니다. 데이터가 다른(비가우스) 분포를 갖는 경우 중앙값은 평균과 매우 다를 수 있으며 기본 모집단의 중심 경향을 더 잘 반영할 수 있습니다.
1 | Median: 50.042 |
분산
분포의 분산은 관측치가 평균값과 얼마나 다르거나 다른지를 나타냅니다.
분산을 분포의 산포의 측도로 생각하는 것이 유용합니다. 분산이 낮으면 평균을 중심으로 그룹화된 값(예: 좁은 종 모양)이 있는 반면, 분산이 높으면 평균에서 분산된 값(예: 넓은 종 모양)이 있습니다.
우리는 낮고 높은 분산을 가진 이상화 된 가우스를 플로팅함으로써 예를 통해 이를 입증 할 수 있습니다. 전체 예제는 다음과 같습니다.
1 2 3 4 5 6 7 8 9 10 11 | # generate and plot gaussians with different variance from numpy import arange from matplotlib import pyplot from scipy.stats import norm # x-axis for the plot x_axis = arange(–3, 3, 0.001) # plot low variance pyplot.plot(x_axis, norm.pdf(x_axis, 0, 0.5)) # plot high variance pyplot.plot(x_axis, norm.pdf(x_axis, 0, 1)) pyplot.show() |
예제를 실행하면 두 개의 이상적인 가우스 분포, 즉 분산이 낮은 파란색이 평균 주위에 그룹화되고 분산이 더 많고 산포가 더 높은 주황색이 표시됩니다.
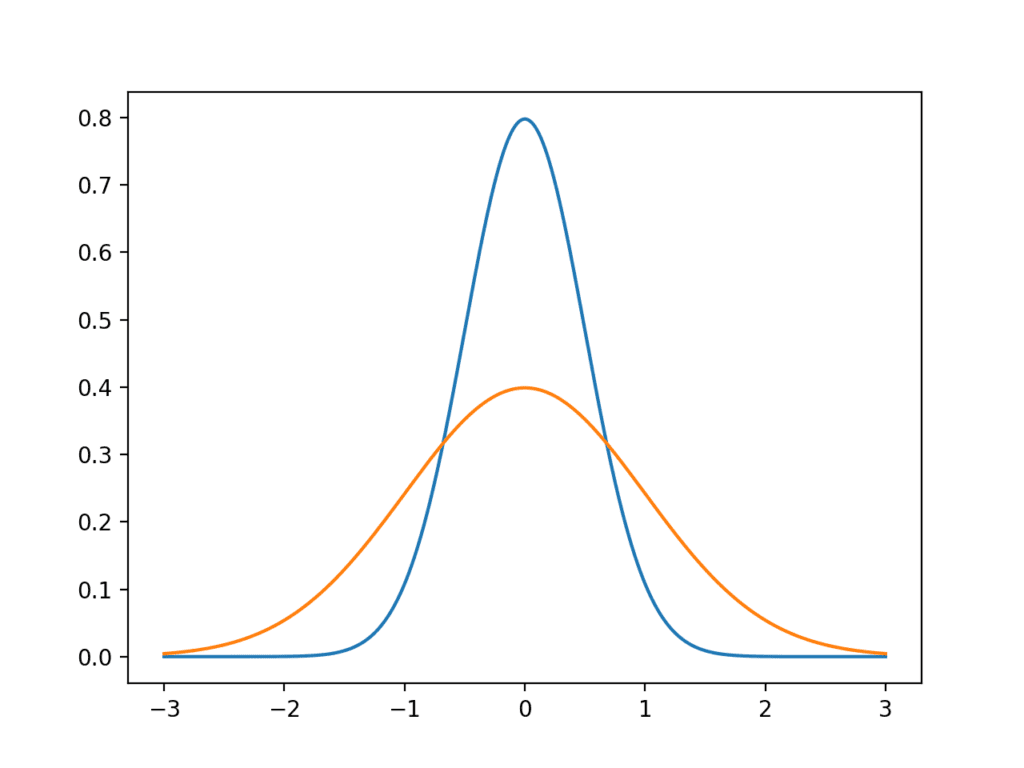
분산이 낮거나 높은 가우스 분포의 선 그림
가우스 분포에서 추출한 데이터 표본의 분산은 표본 평균에서 표본의 각 관측치의 평균 제곱 차이로 계산됩니다.
1 | variance = 1 / (length(data) – 1) * sum(data[i] – mean(data))^2 |
여기서 분산은 종종 측정값의 제곱 단위를 명확하게 보여주는 s^2로 표시됩니다. 관측치 수에서 (-1)이 없는 방정식을 볼 수 있으며, 이는 표본이 아니라 모집단에 대한 분산의 계산입니다.
var()함수를 사용하여 NumPy에서 데이터 샘플의 분산을 계산할 수 있습니다.
아래 예제에서는 테스트 문제에 대한 분산을 계산하는 방법을 보여 줍니다.
1 2 3 4 5 6 7 8 9 10 11 | # calculate the variance of a sample from numpy.random import seed from numpy.random import randn from numpy import var # seed the random number generator seed(1) # generate univariate observations data = 5 * randn(10000) + 50 # calculate variance result = var(data) print(‘Variance: %.3f’ % result) |
예제를 실행하면 분산이 계산되고 인쇄됩니다.
1 | Variance: 24.939 |
분산을 해석하는 것은 단위가 관측치의 제곱 단위이기 때문입니다. 결과의 제곱근을 취하여 관측치의 원래 단위로 단위를 되돌릴 수 있습니다.
예를 들어, 24.939의 제곱근은 약 4.9입니다.
종종 가우스 분포의 확산을 요약할 때 분산의 제곱근을 사용하여 설명됩니다. 이를 표준 편차라고 합니다. 표준 편차는 평균과 함께 가우스 분포를 지정하는 데 필요한 두 가지 주요 모수입니다.
4.9 값은 검정 문제에 대해 표본을 만들 때 지정된 표준 편차 값 5에 매우 가깝다는 것을 알 수 있습니다.
분산 계산을 제곱근으로 래핑하여 표준 편차를 직접 계산할 수 있습니다.
1 | standard deviation = sqrt(1 / (length(data) – 1) * sum(data[i] – mean(data))^2) |
여기서 표준 편차는 종종 s 또는 그리스 소문자 시그마로 작성됩니다.
표준 편차는std() 함수를 통해 배열에 대해 NumPy에서 직접 계산할 수 있습니다.
아래 예는 검정 문제에 대한 표준 편차의 계산을 보여줍니다.
1 2 3 4 5 6 7 8 9 10 11 | # calculate the standard deviation of a sample from numpy.random import seed from numpy.random import randn from numpy import std # seed the random number generator seed(1) # generate univariate observations data = 5 * randn(10000) + 50 # calculate standard deviation result = std(data) print(‘Standard Deviation: %.3f’ % result) |
예제를 실행하면 표본의 표준 편차가 계산되고 인쇄됩니다. 이 값은 분산의 제곱근과 일치하며 문제 정의에 지정된 값인 5.0에 매우 가깝습니다.
1 | Standard Deviation: 4.994 |
분산 측정값은 비가우스 분포에 대해 계산할 수 있지만 일반적으로 해당 분포에 특정한 특수 분산 측정값을 계산할 수 있도록 분포를 식별해야 합니다.
가우스 설명
응용 머신러닝에서는 알고리즘의 결과를 보고해야 하는 경우가 많습니다.
즉, 표본 외 데이터에 대한 모델의 추정된 기술을 보고합니다.
이는 종종 k-fold 교차 검증 또는 다른 반복된 샘플링 절차의 평균 성능을 보고하여 수행됩니다.
모델 기술을 보고할 때 사실상 기술 점수의 분포를 요약하는 것이며 기술 점수는 가우스 분포에서 추출될 가능성이 매우 높습니다.
모델의 평균 성능만 보고하는 것이 일반적입니다. 이것은 모델의 기술 분포에 대한 두 가지 다른 중요한 세부 사항을 숨길 것입니다.
최소한 모델 점수의 가우스 분포와 샘플의 크기의 두 매개 변수를보고하는 것이 좋습니다. 이상적으로는 실제로 모델 기술 점수가 가우스인지 또는 가우스 분포의 매개 변수 보고를 방어할 수 있을 만큼 충분히 가우스처럼 보이는지 확인하는 것도 좋은 생각입니다.
이는 기술 점수의 분포가 독자에 의해 재구성 될 수 있고 잠재적으로 미래에 동일한 문제에 대한 모델의 기술과 비교 될 수 있기 때문에 중요합니다.
확장
이 섹션에는 탐색할 수 있는 자습서를 확장하기 위한 몇 가지 아이디어가 나열되어 있습니다.
- 자체 검정 문제를 개발하고 중심 경향 및 분산 측도를 계산합니다.
- 주어진 데이터 샘플에 대한 요약 보고서를 계산하는 함수를 개발합니다.
- 표준 머신러닝 데이터 세트에 대한 변수 로드 및 요약
이러한 확장 기능을 탐색하면 알고 싶습니다.
추가 정보
이 섹션에서는 더 자세히 알아보려는 경우 주제에 대한 더 많은 리소스를 제공합니다.
증권 시세 표시기
- scipy.stats.norm() API
- numpy.random.seed() API
- numpy.random.randn() API
- matplotlib.pyplot.hist() API
- numpy.mean() API
- numpy.median() API
- numpy.var() API
- numpy.std() API
기사
요약
이 자습서에서는 가우스 분포, 가우스 분포를 식별하는 방법 및 이 분포에서 가져온 데이터의 주요 요약 통계를 계산하는 방법을 알아보았습니다.
특히 다음 내용을 배웠습니다.
- 가우스 분포는 응용 머신러닝 중에 관측된 데이터를 포함하여 많은 관측치에 대해 설명을 제공합니다.
- 분포의 중심 경향이 가장 가능성이 높은 관측치이며 데이터 표본에서 평균 또는 중위수로 추정할 수 있습니다.
- 분산은 분포의 평균으로부터의 평균 편차이며 데이터 표본에서 분산 및 표준 편차로 추정할 수 있습니다.







