라그랑주 승수에 대한 짧은 소개
라그랑주 승수 방법은 같음 또는 부등식 제약 조건이 적용되는 함수의 국소 최소값 또는 국소 최대값을 찾는 간단하고 우아한 방법입니다. 라그랑주 승수는 결정되지 않은 승수라고도합니다. 이 자습서에서는 같음 제약 조건이 지정된 경우이 방법에 대해 설명합니다.
이 튜토리얼에서는 라그랑주 승수의 방법과 같음 제약 조건이 있을 때 함수의 국소 최소값 또는 최대값을 찾는 방법을 알아봅니다.
이 자습서를 완료하면 다음을 알 수 있습니다.
- 같음 제약 조건을 가진 함수의 로컬 최대값 또는 최소값을 찾는 방법
- 같음 제약 조건을 갖는 라그랑주 승수의 방법
튜토리얼 개요
이 튜토리얼은 다음과 같이 두 부분으로 나뉩니다.
- 같음 제약 조건을 갖는 라그랑주 승수의 방법
- 두 가지 해결된 예
필수 구성 요소
이 자습서에서는 사용자가 이미 무엇인지 알고 있다고 가정합니다.
위에 제공된 링크를 클릭하여 이러한 개념을 검토할 수 있습니다.
평등 제약 조건을 가진 라그랑주 승수의 방법은 무엇입니까?
다음과 같은 최적화 문제가 있다고 가정합니다.
f(x) 최소화
대상 :
g_1(x) = 0
g_2(x) = 0
…
g_n(x) = 0
라그랑주 승수의 방법은 먼저 다음 식으로 주어진 라그랑주 함수라는 함수를 구성합니다.
L(x, λ) = f(x) + λ_1 g_1(x) + λ_2 g_2(x) + … + λ_n g_n(x)
여기서 λ는 라그랑주 승수의 벡터를 나타냅니다.
λ = [ λ_1, λ_2, …, λ_n]^T
같음 제약 조건에 따라 f(x)의 국소 최소값을 찾기 위해 라그랑주 함수 L(x, λ)의 정지 점을 찾습니다.
∇xL = 0
∂L/∂λ_i = 0 (i = 1..n의 경우)
따라서 풀어야 할 총 m+n 방정식을 얻습니다.
m = f 도메인의 변수 개수
n = 같음 제약 조건의 수입니다.
요컨대, 국소 최소값은 다음 방정식의 해가 될 것입니다.
∂L / ∂x_j = 0 (j = 1..m의 경우)
g_i(x) = 0 (i = 1..n의 경우)
해결된 예제
이 섹션에는 두 가지 해결 된 예제가 포함되어 있습니다. 이 두 가지를 모두 풀면 라그랑주 승수 방법을 두 개 이상의 변수 함수와 더 많은 수의 같음 제약 조건에 적용하는 방법에 대한 좋은 아이디어를 얻을 수 있습니다.
예제 1: 하나의 같음 제약 조건
다음 최소화 문제를 해결해 보겠습니다.
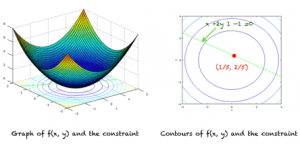
최소화: f(x) = x^2 + y^2
대상 : x + 2y – 1 = 0
첫 번째 단계는 라그랑주 함수를 구성하는 것입니다.
L(x, y, λ) = x^2 + y^2 + λ(x + 2y – 1)
풀어야 할 세 가지 방정식이 있습니다.
∂L/∂x = 0
2x + λ = 0 (1)
∂L/∂y = 0
2년 + 2λ = 0 (2)
∂L/∂λ = 0
x + 2y -1 = 0 (3)
(1)과 (2)를 사용하면 다음을 얻습니다.
λ = -2x = -y
이것을 (3)에 연결하면 다음과 같은 이점이 있습니다.
x = 1/5
y = 2/5
따라서 로컬 최소점은 오른쪽 그림과 같이 (1/5, 2/5)에 있습니다. 왼쪽 그림은 함수의 그래프를 보여줍니다.
함수 그래프(왼쪽). 등고선, 구속조건 및 로컬 최소값(오른쪽)
예제 2: 두 개의 같음 제약 조건
주어진 제약 조건에 따라 다음 함수의 최소값을 찾고 싶다고 가정합니다.
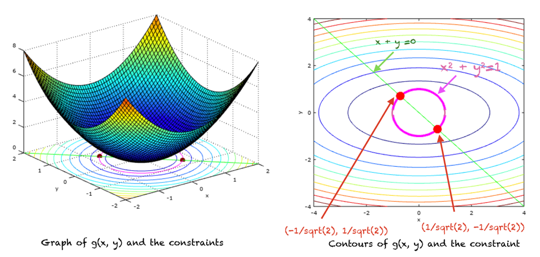
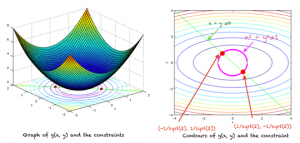
g (x, y) = x ^ 2 + 4y ^ 2 최소화
대상 :
x + y = 0
x^2 + y^2 – 1 = 0
이 문제의 해결책은 먼저 라그랑주 함수를 구성하여 찾을 수 있습니다.
L(x, y, λ_1, λ_2) = x^2 + 4y^2 + λ_1(x + y) + λ_2(x^2 + y^2 – 1)
풀어야 할 4 가지 방정식이 있습니다.
∂L/∂x = 0
2x + λ_1 + 2x λ_2 = 0 (1)
∂L/∂y = 0
8년 + λ_1 + 2년 λ_2 = 0 (2)
∂L/∂λ_1 = 0
x + y = 0 (3)
∂L/∂λ_2 = 0
x^2 + y^2 – 1 = 0 (4)
위의 방정식 시스템을 풀면 (x, y)에 대한 두 가지 해, 즉 두 점을 얻습니다.
(1/제곱(2), -1/제곱(2))
(-1/제곱(2), 1/제곱(2))
함수와 해당 제약 조건 및 로컬 최소값은 다음과 같습니다.
함수 그래프(왼쪽). 등고선, 구속조건 및 로컬 최소값(오른쪽)
최대화 문제와의 관계
최대화하는 함수가 있다면 최대화와 최소화가 동등한 문제라는 것을 명심하면서 비슷한 방식으로 해결할 수 있습니다.
최대화 f (x)는 -f (x)를 최소화하는 것과 같습니다.
머신러닝에서 라그랑주 승수 방법의 중요성
잘 알려진 많은 머신러닝 알고리즘은 라그랑주 승수 방법을 사용합니다. 예를 들어, 주성분 분석(PCA)의 이론적 토대는 같음 제약 조건이 있는 라그랑주 승수 방법을 사용하여 구축됩니다. 마찬가지로 서포트 벡터 머신 SVM의 최적화 문제도 이 방법을 사용하여 해결됩니다. 그러나 SVMS에서는 부등식 제약 조건도 관련됩니다.
확장
이 섹션에는 탐색할 수 있는 자습서를 확장하기 위한 몇 가지 아이디어가 나열되어 있습니다.
- 부등식 제약 조건을 사용한 최적화
- 증권 시세 표시기 조건
- 벡터 머신 지원
요약
이 튜토리얼에서는 라그랑주 승수의 방법이 무엇인지 발견했습니다. 특히 다음 내용을 배웠습니다.
- 라그랑주 승수와 라그랑주 함수
- 같음 제약 조건이 주어질 때 최적화 문제를 해결하는 방법
