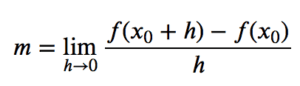튜토리얼 개요

이 자습서는 다음과 같이 두 부분으로 나뉩니다.

1. 선과 곡선의 기울기
2. 곡선에 대한 접선

선의 기울기

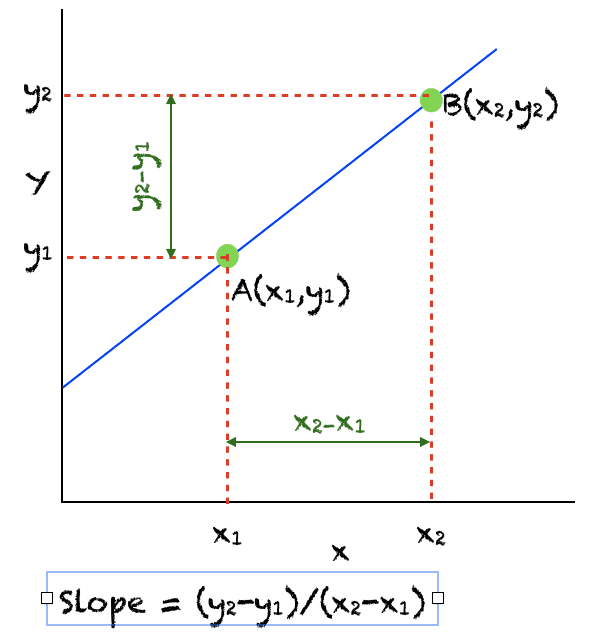
선의 기울기를 검토하는 것으로 시작하겠습니다. 미적분학에서 선의 기울기는 가파름을 숫자로 정의합니다. 이 숫자는 선의 한 지점에서 다른 지점으로 이동할 때 수직 방향의 변화를 수평 방향의 변화로 나누어 계산합니다. 그림은 선의 두 점 A와 B에서 기울기를 계산하는 방법을 보여줍니다.

선의 두 점에서 계산된 선의 기울기

직선은 선의 두 점으로 고유하게 정의할 수 있습니다. 선의 기울기는 선의 모든 곳에서 동일합니다. 따라서 모든 선은 기울기와 선의 한 점으로 고유하게 정의 될 수도 있습니다. 알려진 지점에서 선의 기울기로 정의된 비율에 따라 선의 다른 점으로 이동할 수 있습니다.

곡선의 평균 변화율

선의 기울기에 대한 아이디어를 곡선의 기울기로 확장할 수 있습니다. 아래 그림의 왼쪽 그래프를 고려하십시오. 이 곡선의 ‘가파름’을 측정하려면 곡선의 다른 지점에서 달라질 것입니다. 점 A에서 점 B로 이동할 때의 평균 변화율은 x가 증가할 때 함수의 값이 감소하므로 음수입니다. 점 B에서 점 A로 이동할 때도 마찬가지입니다. 따라서 간격 [x0,x1]에 대해 다음과 같이 정의할 수 있습니다.

(y1-y0)/(x1-x0)

위의 내용은 점 A와 B를 포함하는 시컨트 선의 기울기에 대한 식임을 알 수 있습니다. 기억을 새로 고치기 위해 시컨트 선이 두 점에서 곡선과 교차합니다.

마찬가지로 점 C와 점 D 사이의 평균 변화율은 양수이며 이 두 점을 포함하는 시컨트 선의 기울기로 주어집니다.

구간 대 한 점에 대한 곡선의 변화율

곡선의 기울기 정의

이제 위 그림의 오른쪽 그래프를 살펴 보겠습니다. 점 B를 점 A쪽으로 이동하면 어떻게 됩니까? 새로운 점은 B’라고 부르겠습니다. 점 B’가 A에 무한히 가까울 때 시컨트 선은 곡선에 한 번만 닿는 선으로 바뀝니다. 여기서 B’의 x 좌표는 (x0+h)이고 h는 극히 작은 값입니다. 점 B’의 y 좌표의 해당 값은 (x0+h)에서의 이 함수의 값, 즉 f(x0+h)입니다.

간격 [x0,x0+h]에 대한 평균 변화율은 h가 0에 접근하는 길이 h의 매우 작은 간격에 대한 변화율을 나타냅니다. 이를 점 x0에서 곡선의 기울기라고 합니다. 따라서 임의의 점 A(x0,f(x0))에서 곡선의 기울기는 다음과 같이 정의됩니다.

점 A에서의 곡선 기울기의 표현은 점 x0에서의 f(x)의 도함수와 같습니다. 따라서 도함수를 사용하여 곡선의 기울기를 찾을 수 있습니다. 이 자습서에서 파생(drivatives)의 개념을 검토할 수 있습니다.

곡선의 기울기의 예

다음은 곡선 기울기의 몇 가지 예입니다.

• 임의의 점 k (k≠0)에서 f (x) = 1 / x의 기울기는 (-1 / k ^ 2)로 주어집니다. 예를 들면 다음과 같습니다.
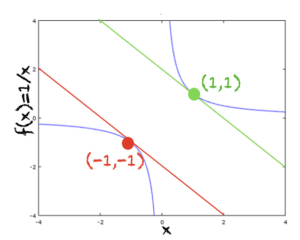
  • (x=2)에서 f(x) = 1/x의 기울기는 -1/4입니다.
  • (x=-1)에서 f(x) = 1/x의 기울기는 -1입니다.
• 임의의 점 k에서 f(x) = x^2의 기울기는 (2k)로 주어집니다. 예를 들어:
  • (x=0)에서 f(x) = x^2의 기울기는 0입니다.
  • (x=1)에서 f(x) = x^2의 기울기는 2입니다.
• f(x) = 2x+1의 기울기는 2와 같은 상수 값입니다. f(x)가 직선을 정의한다는 것을 알 수 있습니다.
• f(x) = k(여기서 k는 상수임)의 기울기는 함수가 어디에서도 변경되지 않으므로 0입니다. 따라서 어느 시점에서든 평균 변화율은 0입니다.

탄젠트 선

앞서 모든 직선은 기울기와 그것을 통과하는 점으로 고유하게 정의 될 수 있다고 언급했습니다. 또한 점 A에서 곡선의 기울기를 정의했습니다. 이 두 가지 사실을 사용하여 점 A(x0,f(x0))에서 곡선 f(x)에 대한 탄젠트를 다음 중 두 가지를 충족하는 선으로 정의합니다.

1. 선은 A를 통과합니다.
2. 선의 기울기는 점 A에서 곡선의 기울기와 같습니다.

위의 두 가지 사실을 사용하여 점 (x0,f(x0))에서 접선의 방정식을 쉽게 결정할 수 있습니다. 다음은 몇 가지 예입니다.

접선의 예

1. f (x) = 1 / x

f (x)의 그래프와 x = 1 및 x = -1에서의 접선이 그림에 나와 있습니다. 다음은 x = 1에서 접선을 결정하는 단계입니다.

f (x) = 1 / x

• 기울기 m과 y-절편 c가 있는 선의 방정식은 y=mx+c로 주어집니다.
• 임의의 점에서 선의 기울기는 함수 f'(x) = -1/x^2로 주어집니다.
• x = 1에서 곡선에 대한 접선의 기울기는 -1이고 y = -x + c가됩니다.
• 접선은 점 (1,1)을 통과하므로 위의 방정식을 대체하면 다음과 같습니다.
  • 1 = -(1)+c ⟹ c = 2
• 접선의 마지막 방정식은 y = -x+2입니다.

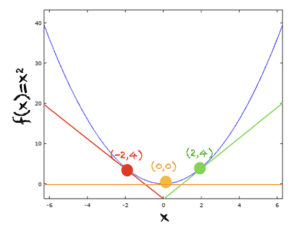
2. f (x) = x ^ 2

아래는 점 x=2, x=-2, x=0의 곡선과 접선입니다. x=0에서 접선은 x=0에서 f(x)의 기울기가 0이므로 x축에 평행합니다.

이것이 x=2에서 접선의 방정식을 계산하는 방법입니다.

f (x) = x ^ 2

• 기울기 m과 y-절편 c가 있는 선의 방정식은 y=mx+c로 주어집니다.
• 임의의 점에서 선의 기울기는 함수 f'(x) = 2x로 주어집니다.
• x = 2에서 곡선에 대한 접선의 기울기는 4이고 y = 4x + c가됩니다.
• 접선은 점 (2,4)를 통과하므로 위의 방정식을 대체하면 다음과 같습니다.
  • 4 = 4(2)+c ⟹ c = -4
• 접선의 최종 방정식은 y = 4x-4입니다.

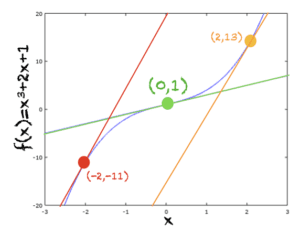
3. f (x) = x ^ 3 + 2x + 1

이 함수는 x=0, x=2 및 x=-2의 접선과 함께 아래에 나와 있습니다. 다음은 x = 0에서 접선의 방정식을 유도하는 단계입니다.

f (x) = x ^ 3 + 2x + 1

• 기울기 m과 y-절편 c가 있는 선의 방정식은 y=mx+c로 주어집니다.
• 임의의 점에서 선의 기울기는 함수 f'(x) = 3x^2+2로 주어집니다.
• x = 0에서 곡선에 대한 접선의 기울기는 2이고 y = 2x + c가됩니다.
• 접선은 점 (0,1)을 통과하므로 위의 방정식을 대체하면 다음과 같습니다.
  • 1 = 2(0)+c ⟹ c = 1
• 접선의 마지막 방정식은 y = 2x+1입니다.

곡선은 x=2와 x=-2 모두에서 동일한 기울기를 가지므로 x=2 및 x=-2의 두 접선은 평행합니다. 모든 x = k 및 x = -k에 대해서도 f'(x) = f'(-x) = 3x ^ 2 + 2와 동일합니다.

확장

이 섹션에는 탐색할 수 있는 자습서를 확장하기 위한 몇 가지 아이디어가 나열되어 있습니다.

• 속도와 가속도
• 함수의 통합

추가 정보

이 섹션에서는 더 자세히 알아보려는 경우 주제에 대한 더 많은 리소스를 제공합니다.

자습서

• 한계와 연속성
• 한계 평가
• 파생 상품

리소스

• 머신러닝을 위한 미적분학 책에 대한 추가 리소스

책

• 토마스의 미적분학, 14판, 2017. (조지 B. 토마스의 원작을 바탕으로 조엘 하스, 크리스토퍼 하일, 모리스 위어 수정)
• 미적분학, 제 3 판, 2017. (길버트 스트랭)
• 미적분학, 8판, 2015. (제임스 스튜어트)

요약

이 튜토리얼에서는 한 점의 곡선 기울기와 한 점의 곡선에 대한 접선의 개념을 발견했습니다.

특히 다음 내용을 배웠습니다.

• 선의 기울기는 얼마입니까?
• 구간 wrt x 동안 곡선의 평균 변화율은 얼마입니까?
• 한 점에서 곡선의 기울기
• 한 점에서 곡선에 접선