파이썬을 사용한 차등 진화 (Differential evolution) 글로벌 최적화

21 12월

파이썬을 사용한 차등 진화 (Differential evolution) 글로벌 최적화

차등 진화(Differential Evolution)는 글로벌 최적화 알고리즘입니다.

진화 알고리즘의 한 유형이며 유전 알고리즘과 같은 다른 진화 알고리즘과 관련이 있습니다.

유전 알고리즘과 달리 비트 문자열 대신 실제 값 숫자의 벡터에서 작동하도록 특별히 설계되었습니다. 또한 유전 알고리즘과 달리 벡터 빼기 및 더하기와 같은 벡터 연산을 사용하여 유전학에서 영감을 얻은 변환 대신 검색 공간을 탐색합니다.

이 자습서에서는 차등 진화 글로벌 최적화 알고리즘을 발견합니다.

이 자습서를 완료하면 다음을 알 수 있습니다.

차등 진화 최적화는 실제 값 후보 솔루션과 함께 작동하도록 설계된 진화 알고리즘 유형입니다.
파이썬에서 차등 진화 최적화 알고리즘 API를 사용하는 방법.
차등 진화를 사용하여 다중 최적으로 전역 최적화 문제를 해결하는 예제입니다.

튜토리얼 개요

이 자습서는 다음과 같이 세 부분으로 나뉩니다.

차등 진화
차등 진화 API
차등 진화 작동 예

차등 진화

차등 진화 또는 줄여서 DE는 확률적 글로벌 검색 최적화 알고리즘입니다.

진화 알고리즘의 한 유형이며 유전 알고리즘과 같은 다른 진화 알고리즘과 관련이 있습니다. 비트 시퀀스를 사용하여 후보 솔루션을 나타내는 유전 알고리즘과 달리 차등 진화은 연속 목적 함수에 대한 다차원 실수 값 후보 솔루션과 함께 작동하도록 설계되었습니다.

차등 진화(DE)는 틀림없이 현재 사용되는 가장 강력한 확률적 실수 파라미터 최적화 알고리즘 중 하나입니다.

— 차등 진화: 최첨단 조사, 2011.

이 알고리즘은 검색에서 기울기 정보를 사용하지 않으므로 미분 비선형 목적 함수에 적합합니다.

이 알고리즘은 실수 값 벡터로 표현되는 후보 솔루션 모집단을 유지하여 작동합니다. 새로운 후보 솔루션은 기존 솔루션의 수정된 버전을 만들어 만들어지며, 이 버전은 알고리즘의 각 반복마다 모집단의 많은 부분을 대체합니다.

새로운 후보 솔루션은 돌연변이가 추가되는 기본 솔루션과 돌연변이의 양과 유형이 계산되는 모집단의 다른 후보 솔루션 (차이 벡터라고)을 선택하는 “전략“을 사용하여 생성됩니다. 예를 들어, 전략은 돌연변이의 차이 벡터에 대한 기본 및 랜덤 솔루션으로 최상의 후보 솔루션을 선택할 수 있습니다.

DE는 두 모집단 벡터 간의 가중 차이를 세 번째 벡터에 추가하여 새 파라미터 벡터를 생성합니다.

— 차등 진화: 연속 공간에 대한 글로벌 최적화를 위한 간단하고 효율적인 휴리스틱, 1997.

기본 솔루션은 자식이 더 나은 목적 함수 평가를 갖는 경우 자식으로 대체됩니다.

마지막으로, 새로운 자식 그룹을 만든 후 각 자식을 해당 자식을 만든 부모와 비교합니다 (각 부모는 단일 자식을 만들었습니다). 자식이 부모보다 낫다면 원래 모집단의 부모를 대체합니다.

— 51페이지, 메타휴리스틱의 본질, 2011.

돌연변이는 후보 솔루션 쌍 간의 차이로 계산되며, 그 결과 차이 벡터가 기본 솔루션에 추가되고 범위 [0,2]의 돌연변이 인자 하이퍼파라미터 세트로 가중치가 부여됩니다.

기본 솔루션의 모든 요소가 변형되는 것은 아닙니다. 이는 재조합 하이퍼파라미터를 통해 제어되며 종종 80%와 같은 큰 값으로 설정되는데, 이는 기본 솔루션의 모든 변수가 아닌 대부분의 변수가 대체됨을 의미합니다. 기본 솔루션에서 값을 유지하거나 대체하는 결정은 이항 또는 지수와 같은 확률 분포를 샘플링하여 각 위치에 대해 개별적으로 결정됩니다.

표준 용어는 다음과 같은 형식으로 차등 전략을 설명하는 데 사용됩니다.

DE/x/y/z

여기서 DE는 “차등 진화“를 나타내고, x는 돌연변이될 기본 해를 정의합니다(예: 무작위 “rand” 또는 모집단에서 최상의 해를 나타내는 경우 “최상”). y는 기본 해에 추가된 차이 벡터의 수(예: 1)를 나타내고, z는 모집단에서 각 해가 유지되는지 또는 대체되는지를 결정하기 위한 확률 분포를 정의합니다(예: 이항의 경우 “bin” 또는 지수의 경우 “exp“).

위에서 사용된 일반적인 규칙은 DE/x/y/z이며, 여기서 DE는 “차등 진화”를 나타내고, x는 교란될 기본 벡터를 나타내는 문자열을 나타내고, y는 x의 섭동에 대해 고려되는 차이 벡터의 수이며, z는 사용되는 크로스오버 유형을 나타냅니다(exp: 지수, bin: 이항).

— 차등 진화: 최첨단 조사, 2011.

DE/best/1/bin 및 DE/best/2/bin 구성은 많은 목적 함수에서 잘 수행되므로 널리 사용되는 구성입니다.

Mezura-Montes et al.이 수행 한 실험은 DE / best / 1 / bin (검색 방향 및 이항 크로스 오버를 찾기 위해 항상 최상의 솔루션을 사용)이 최종 정확도와 결과의 견고성을 기반으로 해결해야 할 문제의 특성에 관계없이 가장 경쟁력있는 체계로 남아 있음을 나타냅니다.

— 차등 진화: 최첨단 조사, 2011.

이제 차등 진화 알고리즘에 익숙해졌으므로 SciPy API 구현을 사용하는 방법을 살펴보겠습니다.

차등 진화 API

차등 진화 전역 최적화 알고리즘은 differential_evolution() SciPy 함수를 통해 파이썬에서 사용할 수 있습니다.

이 함수는 목적 함수의 이름과 각 입력 변수의 한계를 검색의 최소 인수로 사용합니다.

1
2
3
...
# perform the 차등 진화 search
result = differential_evolution(objective, bounds)

검색에 대해 기본값이 있는 여러 가지 추가 하이퍼파라미터가 있지만 검색을 사용자 지정하도록 구성할 수 있습니다.

핵심 하이퍼파라미터는 수행되는 Differential Evolution 검색의 유형을 제어하는 “전략” 인수입니다. 기본적으로 이 설정은 “best1bin“(DE/best/1/bin)으로 설정되며, 이는 대부분의 문제에 적합한 구성입니다. 모집단에서 무작위 솔루션을 선택하고, 다른 솔루션에서 하나를 빼고, 모집단에서 가장 적합한 후보 솔루션에 차이의 스케일 버전을 추가하여 새로운 후보 솔루션을 만듭니다.

새로운 = 최고 + (돌연변이 * (랜드1 – 랜드2))

“popsize” 인수는 모집단에서 유지되는 후보 솔루션의 크기 또는 수를 제어합니다. 후보 솔루션의 차원 수를 나타내는 요소이며 기본적으로 15로 설정됩니다. 즉, 2D 목적 함수의 경우 모집단 크기가 (2 * 15) 또는 30개의 후보 솔루션이 유지됩니다.

알고리즘의 총 반복 횟수는 “maxiter” 인수에 의해 유지되며 기본값은 1,000입니다.

“mutation” 인수는 각 반복마다 후보 솔루션에 대한 변경 횟수를 제어합니다. 기본적으로 이 값은 0.5로 설정됩니다. 재조합의 양은 기본적으로 0.7(지정된 후보 솔루션의 70%)로 설정된 “재조합” 인수를 통해 제어됩니다.

마지막으로, 로컬 검색은 검색의 끝에서 발견된 최상의 후보 솔루션에 적용됩니다. 이는 기본적으로 True로 설정된 “polish” 인수를 통해 제어됩니다.

검색 결과는 사전처럼 속성에 액세스할 수 있는 OptimizeResult 개체입니다. 검색의 성공 여부는 ‘성공‘또는 ‘메시지‘키를 통해 액세스 할 수 있습니다.

총 함수 평가 횟수는 ‘nfev‘를 통해 액세스할 수 있으며 검색을 위해 찾은 최적의 입력은 ‘x‘ 키를 통해 액세스할 수 있습니다.

이제 Python의 차등 진화 API에 익숙해졌으므로 몇 가지 작업 예제를 살펴보겠습니다.

차등 진화 작동 예

이 섹션에서는 도전적인 목적 함수에 차등 진화 알고리즘을 사용하는 예를 살펴보겠습니다.

Ackley 함수는 로컬 검색이 중단될 수 있는 단일 전역 최적값과 여러 로컬 최적값을 갖는 목적 함수의 예입니다.

따라서 전역 최적화 기술이 필요합니다. 이 함수는 전역 최적값이 [0,0]이고 0.0으로 평가되는 2차원 목적 함수입니다.

아래 예제에서는 Ackley를 구현하고 전역 최적값과 다중 국소 최적값을 보여주는 3차원 표면도를 생성합니다.

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
# ackley multimodal function
from numpy import arange
from numpy import exp
from numpy import sqrt
from numpy import cos
from numpy import e
from numpy import pi
from numpy import meshgrid
from matplotlib import pyplot
from mpl_toolkits.mplot3d import Axes3D
 
# objective function
def objective(x, y):
 return –20.0 * exp(–0.2 * sqrt(0.5 * (x**2 + y**2))) – exp(0.5 * (cos(2 * pi * x) + cos(2 * pi * y))) + e + 20
 
# define range for input
r_min, r_max = –5.0, 5.0
# sample input range uniformly at 0.1 increments
xaxis = arange(r_min, r_max, 0.1)
yaxis = arange(r_min, r_max, 0.1)
# create a mesh from the axis
x, y = meshgrid(xaxis, yaxis)
# compute targets
results = objective(x, y)
# create a surface plot with the jet color scheme
figure = pyplot.figure()
axis = figure.gca(projection=‘3d’)
axis.plot_surface(x, y, results, cmap=‘jet’)
# show the plot
pyplot.show()

예제를 실행하면 방대한 수의 국소 최적값을 보여주는 Ackley 함수의 표면도가 생성됩니다.

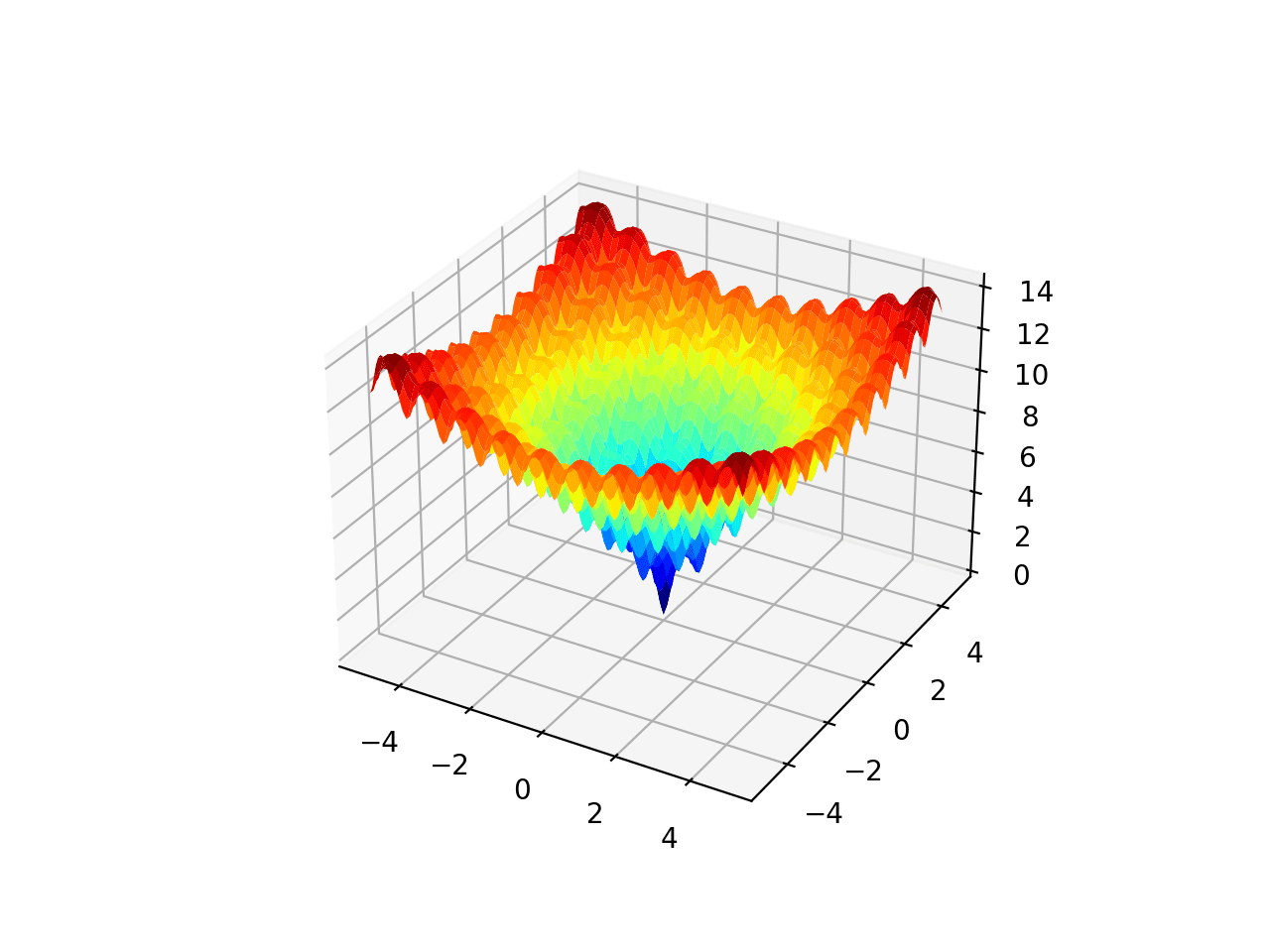
애클리 멀티모달 함수의 3D 표면도

차등 진화 알고리즘을 Ackley 목적 함수에 적용할 수 있습니다.

먼저 검색 공간의 경계를 각 차원에서 함수의 한계로 정의할 수 있습니다.

1
2
3
...
# define the bounds on the search
bounds = [[r_min, r_max], [r_min, r_max]]

그런 다음 목적 함수의 이름과 검색 범위를 지정하여 검색을 적용할 수 있습니다. 이 경우 기본 하이퍼 매개 변수를 사용합니다.

1
2
3
...
# perform the 차등 진화 search
result = differential_evolution(objective, bounds)

검색이 완료되면 검색 상태와 수행된 반복 횟수 및 평가에서 찾은 최상의 결과를 보고합니다.

1
2
3
4
5
6
7
8
...
# summarize the result
print(‘Status : %s’ % result[‘message’])
print(‘Total Evaluations: %d’ % result[‘nfev’])
# evaluate solution
solution = result[‘x’]
evaluation = objective(solution)
print(‘Solution: f(%s) = %.5f’ % (solution, evaluation))

이를 함께 묶어 Ackley 목적 함수에 차등 진화를 적용하는 전체 예가 아래에 나열되어 있습니다.

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
# 차등 진화 global optimization for the ackley multimodal objective function
from scipy.optimize import differential_evolution
from numpy.random import rand
from numpy import exp
from numpy import sqrt
from numpy import cos
from numpy import e
from numpy import pi
 
# objective function
def objective(v):
 x, y = v
 return –20.0 * exp(–0.2 * sqrt(0.5 * (x**2 + y**2))) – exp(0.5 * (cos(2 * pi * x) + cos(2 * pi * y))) + e + 20
 
# define range for input
r_min, r_max = –5.0, 5.0
# define the bounds on the search
bounds = [[r_min, r_max], [r_min, r_max]]
# perform the 차등 진화 search
result = differential_evolution(objective, bounds)
# summarize the result
print(‘Status : %s’ % result[‘message’])
print(‘Total Evaluations: %d’ % result[‘nfev’])
# evaluate solution
solution = result[‘x’]
evaluation = objective(solution)
print(‘Solution: f(%s) = %.5f’ % (solution, evaluation))

예제를 실행하면 최적화가 실행되고 결과가 보고됩니다.

참고: 결과는 알고리즘 또는 평가 절차의 확률적 특성 또는 수치 정밀도의 차이에 따라 달라질 수 있습니다. 예제를 몇 번 실행하고 평균 결과를 비교하는 것이 좋습니다.

이 경우 알고리즘이 입력값이 0이고 목적 함수 평가가 0인 최적값을 찾았음을 알 수 있습니다.

총 3,063 개의 기능 평가가Differential Evolution 수행되었음을 알 수 있습니다.

1
2
3
Status: Optimization terminated successfully.
Total Evaluations: 3063
Solution: f([0. 0.]) = 0.00000

추가 정보

이 섹션에서는 더 자세히 알아보려는 경우 주제에 대한 더 많은 리소스를 제공합니다.

논문

책

증권 시세 표시기

scipy.optimize.differential_evolution API를 사용합니다.
scipy.optimize.OptimizeResult API.

기사

차등 진화, 위키 백과.

요약

이 자습서에서는 차등 진화 전역 최적화 알고리즘을 발견했습니다.

특히 다음 내용을 배웠습니다.

Differential Evolution 최적화는 실제 값 후보 솔루션과 함께 작동하도록 설계된 진화 알고리즘 유형입니다.
파이썬에서 차등 진화 최적화 알고리즘 API를 사용하는 방법.
차등 진화를 사용하여 다중 최적으로 전역 최적화 문제를 해결하는 예제입니다.

Tags:

Differential Evolution Global Optimization,Machine learning