몇 줄의 코드로 구현할 수 있는 간단하고 효과적인 기술입니다. 또한 더 나은 성능을 가져올 수 있는 많은 확장 및 수정의 기반을 제공합니다. 이 알고리즘은 또한 딥 러닝 신경망을 훈련하는 데 사용되는 확률적 경사하강법이라는 널리 사용되는 확장의 기초를 제공합니다.
이 튜토리얼에서는 경사하강법 최적화를 처음부터 구현하는 방법을 알아봅니다.
이 자습서를 완료하면 다음을 알 수 있습니다.
경사하강법 최적화
경사하강법은 최적화 알고리즘입니다.
기술적으로 1차 최적화 알고리즘이라고 하며, 목표 목적 함수의 1차 도함수를 명시적으로 사용합니다.
1 차 방법은 그래디언트 정보에 의존하여 검색을 최소값으로 안내합니다 …
— 69페이지, 최적화 알고리즘, 2019.
1차 도함수 또는 간단히 “도함수”는 예를 들어 특정 입력에 대한 특정 지점에서 목표 함수의 변화율 또는 기울기입니다.
대상 함수가 여러 입력 변수를 취하는 경우 이를 다변량 함수라고 하며 입력 변수를 벡터로 생각할 수 있습니다. 차례로, 다변량 대상 함수의 도함수는 또한 벡터로서 취해질 수 있으며, 일반적으로 “그래디언트“로 지칭됩니다.
- 기울기: 다변량 목적 함수에 대한 1차 도함수입니다.
도함수 또는 기울기는 입력값에 대한 목표 함수의 가장 가파른 상승 방향입니다.
특히, 그래디언트의 부호는 대상 함수가 해당 지점에서 증가하는지 감소하는지 알려줍니다.
- 양의 기울기: 그 시점에서 함수가 증가하고 있습니다.
- 음의 그라디언트: 해당 시점에서 함수가 감소합니다.
경사하강법은 함수의 최소값을 찾기 위해 대상 함수의 기울기 내리막의 음수를 따르는 최소화 최적화 알고리즘을 말합니다.
유사하게, 우리는 목표 함수의 최대값까지 기울기 오르막을 따르는 최적화 알고리즘의 최대화 버전에 대해 기울기 상승을 참조할 수 있습니다.
- 경사하강법: 기울기의 음수를 목표 함수의 최소값으로 따르는 최소화 최적화입니다.
- 기울기 상승: 기울기를 따라 목표 함수의 최대값까지 최대화 최적화입니다.
경사하강법 알고리즘의 핵심은 대상 함수의 기울기를 따르는 아이디어입니다.
정의에 따라 최적화 알고리즘은 미분 함수를 사용할 수 있고 모든 입력 값에 대해 계산할 수 있는 대상 함수에만 적합합니다. 이것은 모든 대상 함수에 적용되는 것이 아니라 소위 미분 가능한 함수에만 적용됩니다.
경사하강법 알고리즘의 주요 이점은 구현하기 쉽고 광범위한 최적화 문제에 효과적이라는 것입니다.
그라데이션 메서드는 구현하기 쉽고 종종 잘 수행됩니다.
— 페이지 115, 최적화 소개, 2001.
경사하강법은 1차 도함수를 사용하여 목표 함수의 최적값(최소값 또는 최대값)으로 이동하는 알고리즘 계열을 나타냅니다.
일반적으로 알고리즘에 추가된 피처에 따라 이름이 지정된 기본 접근 방식에는 모멘텀이 있는 경사하강법, 적응형 경사가 있는 경사하강법 등과 같은 많은 확장이 있습니다.
경사하강법은 확률적 경사하강법 또는 SGD라고 하는 딥러닝 신경망을 훈련하는 데 사용되는 최적화 알고리즘의 기초이기도 합니다. 이 변형에서 대상 함수는 오차 함수이고 함수 기울기는 문제 도메인의 표본에 대한 예측 오차에서 근사됩니다.
이제 경사하강법 최적화에 대한 높은 수준의 아이디어에 익숙해졌으므로 알고리즘을 구현하는 방법을 살펴보겠습니다.
경사하강법 알고리즘
이 섹션에서는 경사하강법 알고리즘을 자세히 살펴보겠습니다.
경사하강법 알고리즘에는 최적화되는 목표 함수와 목표 함수에 대한 미분 함수가 필요합니다.
목표 함수 f()는 주어진 입력 세트에 대한 점수를 반환하고, 미분 함수 f'()는 주어진 입력 세트에 대한 타겟 함수의 도함수를 제공합니다.
- 목적 함수: 주어진 입력 파라미터 세트에 대한 점수를 계산합니다.
미분 함수: 주어진 입력 집합에 대한 목적 함수의 도함수(기울기)를 계산합니다.
경사하강법 알고리즘에는 입력 공간에서 임의로 선택된 점과 같이 문제의 시작점(x)이 필요합니다.
그런 다음 미분이 계산되고 목표 함수를 최소화한다고 가정할 때 목표 함수에서 내리막 이동이 발생할 것으로 예상되는 입력 공간에서 한 걸음을 수행합니다.
내리막 이동은 먼저 입력 공간에서 이동할 거리를 계산하여 이루어지며, 단계 크기(알파 또는 학습률이라고 함)에 기울기를 곱하여 계산됩니다. 그런 다음 현재 지점에서 빼서 그라디언트에 대해 이동하거나 대상 함수 아래로 이동합니다.
주어진 점에서 목적 함수가 가파를수록 기울기의 크기가 커지고 검색 공간에서 취해지는 단계가 커집니다.
수행된 단계의 크기는 단계 크기 하이퍼파라미터를 사용하여 조정됩니다.
- 단계 크기(알파): 알고리즘의 각 반복에 대해 기울기에 대해 검색 공간에서 이동할 거리를 제어하는 하이퍼 매개 변수입니다.
단계 크기가 너무 작 으면 검색 공간에서의 움직임이 작아지고 검색 시간이 오래 걸립니다. 단계 크기가 너무 크면 검색이 검색 공간을 돌아다니며 최적 단계를 건너뛸 수 있습니다.
매우 작은 단계를 수행하고 모든 단계에서 기울기를 재평가하거나 매번 큰 단계를 수행 할 수 있습니다. 첫 번째 접근 방식은 최소화 장치에 도달하는 힘든 방법을 초래하는 반면, 두 번째 접근 방식은 최소화 장치에 대한 더 지그재그 경로를 초래할 수 있습니다.
— 페이지 114, 최적화 소개, 2001.
적절한 스텝 크기를 찾으려면 특정 대상 함수에 대해 시행착오가 필요할 수 있습니다.
스텝 크기를 선택하는 어려움으로 인해 대상 함수의 정확한 최적값을 찾기가 어려울 수 있습니다. 많은 확장에는 알고리즘이 함수 최적을 연마할 수 있도록 시간이 지남에 따라 학습률을 조정하여 다른 차원에서 더 작은 단계 또는 다른 크기의 단계를 수행하는 등의 작업이 포함됩니다.
점의 미분을 계산하고 입력 공간에서 새로운 점을 계산하는 과정은 일부 정지 조건이 충족 될 때까지 반복됩니다. 이는 고정된 수의 스텝 또는 목표 함수 평가, 일부 반복 횟수에 대한 목표 함수 평가의 개선 부족 또는 기울기 0으로 표시되는 검색 공간의 평탄한(고정) 영역 식별일 수 있습니다.
- 정지 조건: 검색 절차를 종료할 시기를 결정합니다.
Python에서 경사하강법 알고리즘을 구현하는 방법을 살펴보겠습니다.
먼저, 초기 점을 경계로 정의된 입력 공간에서 임의로 선택된 점으로 정의할 수 있습니다.
한계는 목적 함수와 함께 각 차원에 대한 최소값과 최대값이 있는 배열로 정의할 수 있습니다. rand() NumPy 함수를 사용하여 0-1 범위의 난수 벡터를 생성할 수 있습니다.
| ... # generate an initial point solution = bounds[:, 0] + rand(len(bounds)) * (bounds[:, 1] – bounds[:, 0]) |
그런 다음 derivative()라는 함수를 사용하여 점의 도함수를 계산할 수 있습니다.
| ... # calculate gradient gradient = derivative(solution) |
그리고 검색 공간에서 현재 지점의 언덕 아래 새로운 지점으로 한 걸음 내딛습니다.
새 위치는 계산된 기울기와 step_size 하이퍼파라미터를 사용하여 계산됩니다.
| ... # take a step solution = solution – step_size * gradient |
그런 다음이 점을 평가하고 성과를보고 할 수 있습니다.
| ... # evaluate candidate point solution_eval = objective(solution) |
이 프로세스는 n_iter 하이퍼파라미터를 통해 제어되는 고정된 반복 횟수에 대해 반복될 수 있습니다.
| ... # run the gradient descent for i in range(n_iter): # calculate gradient gradient = derivative(solution) # take a step solution = solution – step_size * gradient # evaluate candidate point solution_eval = objective(solution) # report progress print(‘>%d f(%s) = %.5f’ % (i, solution, solution_eval)) |
이 모든 것을 gradient_descent()라는 함수로 묶을 수 있습니다.
이 함수는 목적 함수와 기울기 함수의 이름뿐만 아니라 목적 함수에 대한 입력값의 한계, 반복 횟수 및 스텝 크기를 취한 다음, 검색이 끝날 때 해와 그 평가를 반환합니다.
함수로 구현된 완전한 경사하강법 최적화 알고리즘은 다음과 같습니다.
| # gradient descent algorithm
def gradient_descent(objective, derivative, bounds, n_iter, step_size):
# generate an initial point
solution = bounds[:, 0] + rand(len(bounds)) * (bounds[:, 1] – bounds[:, 0])
# run the gradient descent
for i in range(n_iter):
# calculate gradient
gradient = derivative(solution)
# take a step
solution = solution – step_size * gradient
# evaluate candidate point
solution_eval = objective(solution)
# report progress
print(‘>%d f(%s) = %.5f’ % (i, solution, solution_eval))
return [solution, solution_eval]
|
이제 경사하강법 알고리즘에 익숙해졌으므로 작업 예제를 살펴보겠습니다.
경사하강법 작동 예
이 섹션에서는 간단한 테스트 최적화 함수에 경사하강법을 적용하는 예제를 살펴보겠습니다.
먼저 최적화 함수를 정의해 보겠습니다.
입력을 제곱하고 -1.0에서 1.0까지의 유효한 입력 범위를 정의하는 간단한 1 차원 함수를 사용합니다.
아래의 objective()함수는이 함수를 구현합니다.
| # objective function def objective(x): return x**2.0 |
그런 다음 범위의 모든 입력을 샘플링하고 각각에 대한 목적 함수 값을 계산할 수 있습니다.
| ... # define range for input r_min, r_max = –1.0, 1.0 # sample input range uniformly at 0.1 increments inputs = arange(r_min, r_max+0.1, 0.1) # compute targets results = objective(inputs) |
마지막으로 입력(x축) 대 목적 함수 값(y축)의 선 플롯을 만들어 검색할 목적 함수의 모양에 대한 직관을 얻을 수 있습니다.
| ... # create a line plot of input vs result pyplot.plot(inputs, results) # show the plot pyplot.show() |
아래 예제는 이를 함께 연결하고 1차원 테스트 함수를 플로팅하는 예를 제공합니다.
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 | # plot of simple function from numpy import arange from matplotlib import pyplot # objective function def objective(x): return x**2.0 # define range for input r_min, r_max = –1.0, 1.0 # sample input range uniformly at 0.1 increments inputs = arange(r_min, r_max+0.1, 0.1) # compute targets results = objective(inputs) # create a line plot of input vs result pyplot.plot(inputs, results) # show the plot pyplot.show() |
예제를 실행하면 함수에 대한 입력값(x-축)과 함수의 계산된 출력값(y-축)의 선 플롯이 생성됩니다.
우리는 포물선이라고 불리는 친숙한 U 자형을 볼 수 있습니다.
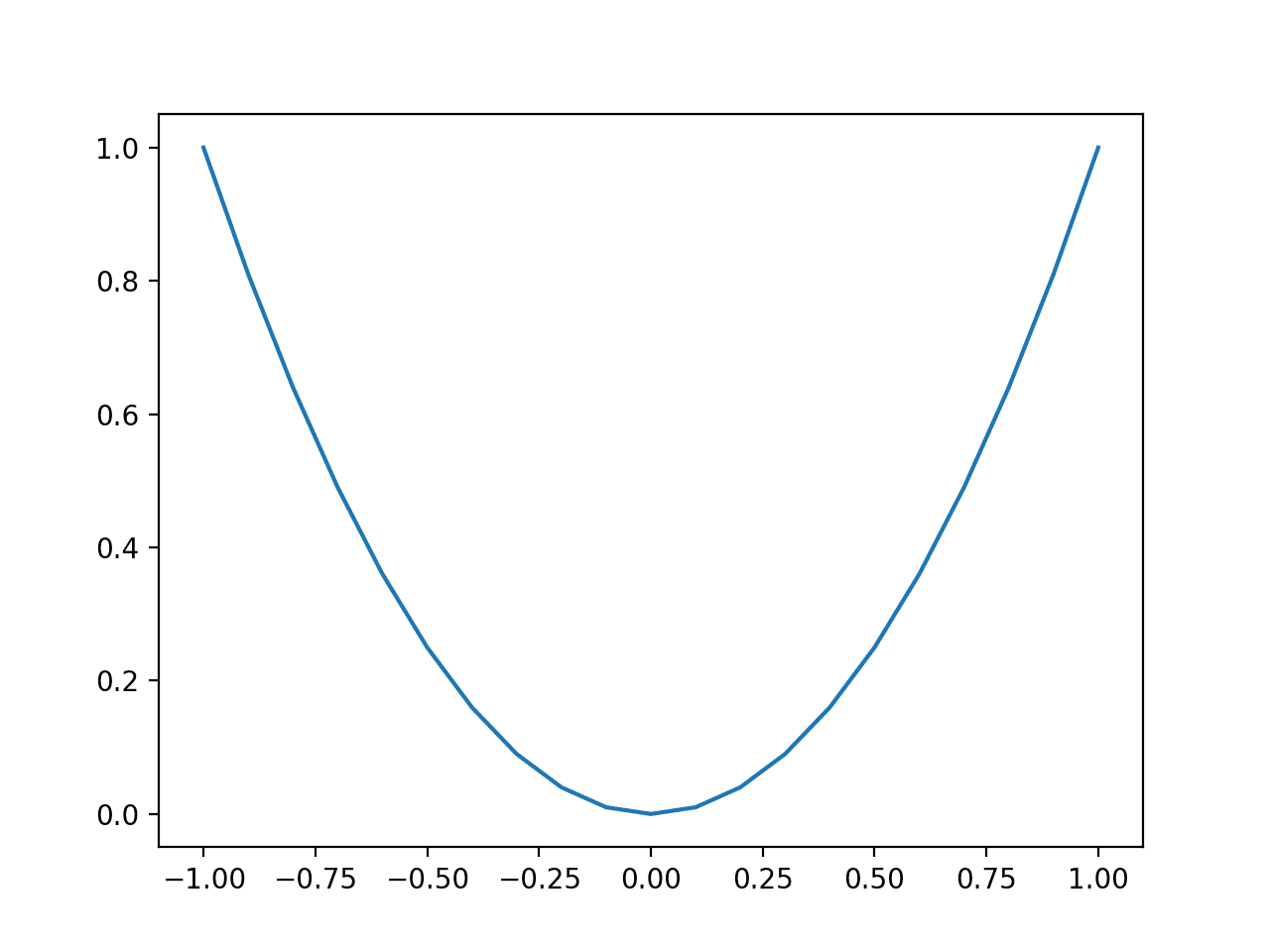
단순 <>차원 함수의 선 플롯
다음으로 경사하강법 알고리즘을 문제에 적용할 수 있습니다.
먼저이 함수의 도함수를 계산하는 함수가 필요합니다.
x^2의 도함수는 x * 2이고 derivative() 함수는 이를 아래에서 구현합니다.
| # derivative of objective function def derivative(x): return x * 2.0 |
그런 다음 목적 함수의 한계, 스텝 크기 및 알고리즘의 반복 횟수를 정의할 수 있습니다.
0.1 및 30 반복의 단계 크기를 사용하며 둘 다 약간의 실험 후에 발견되었습니다.
| ... # define range for input bounds = asarray([[–1.0, 1.0]]) # define the total iterations n_iter = 30 # define the maximum step size step_size = 0.1 # perform the gradient descent search best, score = gradient_descent(objective, derivative, bounds, n_iter, step_size) |
이를 함께 묶어 1차원 테스트 함수에 경사하강법 최적화를 적용하는 전체 예가 아래에 나열되어 있습니다.
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 | # example of gradient descent for a one-dimensional function
from numpy import asarray
from numpy.random import rand
# objective function
def objective(x):
return x**2.0
# derivative of objective function
def derivative(x):
return x * 2.0
# gradient descent algorithm
def gradient_descent(objective, derivative, bounds, n_iter, step_size):
# generate an initial point
solution = bounds[:, 0] + rand(len(bounds)) * (bounds[:, 1] – bounds[:, 0])
# run the gradient descent
for i in range(n_iter):
# calculate gradient
gradient = derivative(solution)
# take a step
solution = solution – step_size * gradient
# evaluate candidate point
solution_eval = objective(solution)
# report progress
print(‘>%d f(%s) = %.5f’ % (i, solution, solution_eval))
return [solution, solution_eval]
# define range for input
bounds = asarray([[–1.0, 1.0]])
# define the total iterations
n_iter = 30
# define the step size
step_size = 0.1
# perform the gradient descent search
best, score = gradient_descent(objective, derivative, bounds, n_iter, step_size)
print(‘Done!’)
print(‘f(%s) = %f’ % (best, score))
|
예제를 실행하면 검색 공간의 임의의 지점에서 시작한 다음 경사하강법 알고리즘을 적용하여 성능을 보고합니다.
참고: 결과는 알고리즘 또는 평가 절차의 확률적 특성 또는 수치 정밀도의 차이에 따라 달라질 수 있습니다. 예제를 몇 번 실행하고 평균 결과를 비교하는 것이 좋습니다.
이 경우 알고리즘이 약 0.0의 함수 평가로 약 20-30 회 반복 후에 좋은 솔루션을 찾는다는 것을 알 수 있습니다. 이 함수의 최적값은 f(0.0) = 0.0입니다.
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 | >0 f([-0.36308639]) = 0.13183 >1 f([-0.29046911]) = 0.08437 >2 f([-0.23237529]) = 0.05400 >3 f([-0.18590023]) = 0.03456 >4 f([-0.14872018]) = 0.02212 >5 f([-0.11897615]) = 0.01416 >6 f([-0.09518092]) = 0.00906 >7 f([-0.07614473]) = 0.00580 >8 f([-0.06091579]) = 0.00371 >9 f([-0.04873263]) = 0.00237 >10 f([-0.0389861]) = 0.00152 >11 f([-0.03118888]) = 0.00097 >12 f([-0.02495111]) = 0.00062 >13 f([-0.01996089]) = 0.00040 >14 f([-0.01596871]) = 0.00025 >15 f([-0.01277497]) = 0.00016 >16 f([-0.01021997]) = 0.00010 >17 f([-0.00817598]) = 0.00007 >18 f([-0.00654078]) = 0.00004 >19 f([-0.00523263]) = 0.00003 >20 f([-0.0041861]) = 0.00002 >21 f([-0.00334888]) = 0.00001 >22 f([-0.0026791]) = 0.00001 >23 f([-0.00214328]) = 0.00000 >24 f([-0.00171463]) = 0.00000 >25 f([-0.0013717]) = 0.00000 >26 f([-0.00109736]) = 0.00000 >27 f([-0.00087789]) = 0.00000 >28 f([-0.00070231]) = 0.00000 >29 f([-0.00056185]) = 0.00000 Done! f([-0.00056185]) = 0.000000 |
이제 좋은 스텝 크기의 중요성에 대해 알아보겠습니다.
단계 크기를 큰 값(예: 1.0)으로 설정하고 검색을 다시 실행합니다.
| ... # define the step size step_size = 1.0 |
더 큰 단계 크기로 예제를 실행하고 결과를 검사합니다.
참고: 결과는 알고리즘 또는 평가 절차의 확률적 특성 또는 수치 정밀도의 차이에 따라 달라질 수 있습니다. 예제를 몇 번 실행하고 평균 결과를 비교하는 것이 좋습니다.
검색이 최적값을 찾지 못하고 대신 도메인 주위를 바운스하는 것을 볼 수 있습니다(이 경우 값 0.64820935와 -0.64820935 사이)..
| … >25 f([0.64820935]) = 0.42018 >26 f([-0.64820935]) = 0.42018 >27 f([0.64820935]) = 0.42018 >28 f([-0.64820935]) = 0.42018 >29 f([0.64820935]) = 0.42018 Done! f([0.64820935]) = 0.420175 |
이제 1e-8과 같이 훨씬 작은 스텝 크기를 시도하십시오..
| ... # define the step size step_size = 1e–5 |
참고: 결과는 알고리즘 또는 평가 절차의 확률적 특성 또는 수치 정밀도의 차이에 따라 달라질 수 있습니다. 예제를 몇 번 실행하고 평균 결과를 비교하는 것이 좋습니다.
검색을 다시 실행하면 알고리즘이 시작점에서 목적 함수의 기울기 아래로 매우 느리게 이동하는 것을 볼 수 있습니다.
| … >25 f([-0.87315153]) = 0.76239 >26 f([-0.87313407]) = 0.76236 >27 f([-0.8731166]) = 0.76233 >28 f([-0.87309914]) = 0.76230 >29 f([-0.87308168]) = 0.76227 Done! f([-0.87308168]) = 0.762272 |
이 두 가지 간단한 예제에서는 너무 크거나 너무 작은 스텝 크기를 선택할 때의 문제점과 주어진 목적 함수에 대해 다양한 스텝 크기 값을 테스트하는 것의 일반적인 중요성을 강조합니다.
마지막으로 학습률을 다시 0.1로 변경하고 대상 함수의 플롯에서 검색 진행률을 시각화할 수 있습니다.
먼저gradient_descent()함수를 업데이트하여 최적화 중에 발견 된 모든 솔루션과 점수를 목록으로 저장하고 찾은 최상의 솔루션 대신 검색이 끝날 때 반환 할 수 있습니다.
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 | # gradient descent algorithm
def gradient_descent(objective, derivative, bounds, n_iter, step_size):
# track all solutions
solutions, scores = list(), list()
# generate an initial point
solution = bounds[:, 0] + rand(len(bounds)) * (bounds[:, 1] – bounds[:, 0])
# run the gradient descent
for i in range(n_iter):
# calculate gradient
gradient = derivative(solution)
# take a step
solution = solution – step_size * gradient
# evaluate candidate point
solution_eval = objective(solution)
# store solution
solutions.append(solution)
scores.append(solution_eval)
# report progress
print(‘>%d f(%s) = %.5f’ % (i, solution, solution_eval))
return [solutions, scores]
|
함수를 호출 할 수 있으며 검색 중에 찾은 솔루션 목록과 점수를 얻을 수 있습니다.
| ... # perform the gradient descent search solutions, scores = gradient_descent(objective, derivative, bounds, n_iter, step_size) |
이전과 같이 목적 함수의 선 그림을 만들 수 있습니다.
| ... # sample input range uniformly at 0.1 increments inputs = arange(bounds[0,0], bounds[0,1]+0.1, 0.1) # compute targets results = objective(inputs) # create a line plot of input vs result pyplot.plot(inputs, results) |
마지막으로 찾은 각 솔루션을 빨간색 점으로 표시하고 점을 선으로 연결하여 검색이 내리막 길을 어떻게 이동했는지 확인할 수 있습니다.
| ... # plot the solutions found pyplot.plot(solutions, scores, ‘.-‘, color=‘red’) |
이 모든 것을 하나로 묶어 1차원 테스트 함수에서 경사하강법 검색 결과를 플로팅하는 전체 예가 아래에 나열되어 있습니다.
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 | # example of plotting a gradient descent search on a one-dimensional function
from numpy import asarray
from numpy import arange
from numpy.random import rand
from matplotlib import pyplot
# objective function
def objective(x):
return x**2.0
# derivative of objective function
def derivative(x):
return x * 2.0
# gradient descent algorithm
def gradient_descent(objective, derivative, bounds, n_iter, step_size):
# track all solutions
solutions, scores = list(), list()
# generate an initial point
solution = bounds[:, 0] + rand(len(bounds)) * (bounds[:, 1] – bounds[:, 0])
# run the gradient descent
for i in range(n_iter):
# calculate gradient
gradient = derivative(solution)
# take a step
solution = solution – step_size * gradient
# evaluate candidate point
solution_eval = objective(solution)
# store solution
solutions.append(solution)
scores.append(solution_eval)
# report progress
print(‘>%d f(%s) = %.5f’ % (i, solution, solution_eval))
return [solutions, scores]
# define range for input
bounds = asarray([[–1.0, 1.0]])
# define the total iterations
n_iter = 30
# define the step size
step_size = 0.1
# perform the gradient descent search
solutions, scores = gradient_descent(objective, derivative, bounds, n_iter, step_size)
# sample input range uniformly at 0.1 increments
inputs = arange(bounds[0,0], bounds[0,1]+0.1, 0.1)
# compute targets
results = objective(inputs)
# create a line plot of input vs result
pyplot.plot(inputs, results)
# plot the solutions found
pyplot.plot(solutions, scores, ‘.-‘, color=’red’)
# show the plot
pyplot.show()
|
예제를 실행하면 이전과 같이 목적 함수에 대해 경사하강법 검색을 수행하지만, 이 경우 검색 중에 발견된 각 점이 플로팅됩니다.
참고: 결과는 알고리즘 또는 평가 절차의 확률적 특성 또는 수치 정밀도의 차이에 따라 달라질 수 있습니다. 예제를 몇 번 실행하고 평균 결과를 비교하는 것이 좋습니다.
이 경우 검색이 함수의 왼쪽 부분 중간쯤에서 시작되어 분지 바닥까지 내리막길을 밟았음을 알 수 있습니다.
곡선이 더 큰 목적 함수 부분에서 도함수(기울기)가 더 크고 차례로 더 큰 단계가 수행된다는 것을 알 수 있습니다. 마찬가지로, 최적에 가까워질수록 기울기가 더 작아지고 차례로 더 작은 단계가 수행됩니다.
이는 스텝 크기가 목적 함수의 기울기(곡률) 크기에 대한 스케일 인수로 사용된다는 것을 강조합니다.
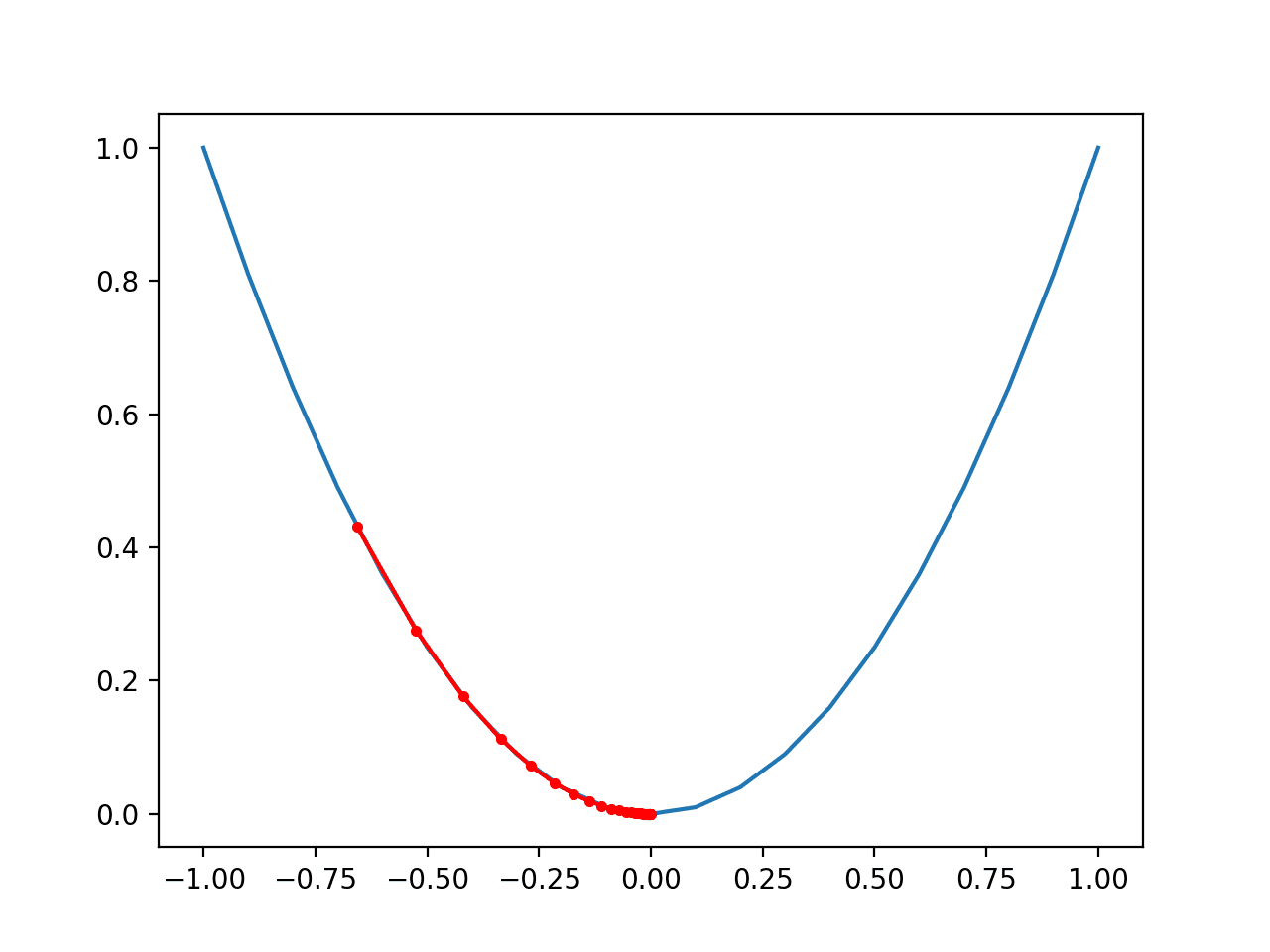
1차원 목적 함수에 대한 경사하강법의 진행 플롯
추가 정보
이 섹션에서는 더 자세히 알아보려는 경우 주제에 대한 더 많은 리소스를 제공합니다.
책
증권 시세 표시기
기사
요약
이 자습서에서는 경사하강법 최적화를 처음부터 구현하는 방법을 알아보았습니다.
특히 다음 내용을 배웠습니다.
- 경사하강법은 미분 가능한 목적 함수를 최적화하기 위한 일반적인 절차입니다.
- Python에서 경사하강법 알고리즘을 처음부터 구현하는 방법.
- 경사하강법 알고리즘을 목적 함수에 적용하는 방법.









