머신러닝의 통계적 허용 오차 구간에 대한 짧은 소개

07 12월

머신러닝의 통계적 허용 오차 구간에 대한 짧은 소개

by Nepirity

in Technology

Comments

데이터에 상한과 하한을 두는 것이 유용할 수 있습니다.

이러한 경계는 변칙을 식별하고 예상되는 사항에 대한 기대치를 설정하는 데 사용할 수 있습니다. 모집단의 관측치에 대한 한계를 공차 구간이라고 합니다. 공차 구간은 추정 통계량 필드에서 나옵니다.

공차 구간은 단일 예측값에 대한 불확실성을 정량화하는 예측 구간과 다릅니다. 또한 평균과 같은 모집단 모수의 불확실성을 정량화하는 신뢰 구간과도 다릅니다. 대신, 공차 구간은 모집단 분포의 일부를 포함합니다.

이 자습서에서는 통계적 공차 구간과 가우스 데이터에 대한 공차 구간을 계산하는 방법을 알아봅니다.

이 자습서를 완료하면 다음을 알 수 있습니다.

이 통계적 공차 구간은 모집단의 관측치에 대한 한계를 제공합니다.
공차 구간을 사용하려면 커버리지 비율과 신뢰 수준을 모두 지정해야 합니다.
가우스 분포를 갖는 데이터 샘플에 대한 허용 오차 구간을 쉽게 계산할 수 있습니다.

튜토리얼 개요

이 튜토리얼은 다음과 같이 네 부분으로 나뉩니다.:

데이터의 경계
통계적 공차 구간이란?
공차 구간 계산 방법
가우스 분포에 대한 공차 구간

데이터의 경계

데이터에 경계를 두는 것이 유용합니다.

예를 들어 도메인의 데이터 샘플이 있는 경우 정규값의 상한과 하한을 알면 데이터의 변칙 또는 이상값을 식별하는 데 도움이 될 수 있습니다.

예측을 수행하는 프로세스 또는 모델의 경우 합리적인 예측이 취할 수 있는 예상 범위를 아는 것이 도움이 될 수 있습니다.

일반적인 값 범위를 알면 기대치를 설정하고 변칙을 감지하는 데 도움이 될 수 있습니다.

데이터에 대한 공통값의 범위를 공차 구간이라고 합니다.

통계적 공차 구간이란?

공차 구간은 모집단의 데이터 비율 추정치에 대한 한계입니다.

통계적 공차 구간은 표본 추출된 모집단이나 공정에서 추출된 단위의 지정된 비율을 [포함]합니다.

— 3페이지, 통계 간격: 실무자 및 연구자를 위한 가이드, 2017.

구간은 표본 추출 오차와 모집단 분포의 분산에 의해 제한됩니다. 큰 수의 법칙이 주어지면 표본 크기가 증가할수록 확률이 기본 모집단 분포와 더 잘 일치합니다.

다음은 명시된 공차 간격의 예입니다.

x에서 y까지의 범위는 99%의 신뢰도로 데이터의 95%를 포함합니다.

데이터가 가우스인 경우 간격은 평균값의 컨텍스트에서 표현될 수 있습니다. 예를 들어:

x +/- y는 99%의 신뢰도로 데이터의 95%를 다룹니다.

이러한 구간을 통계적 공차 구간이라고 부르며, 설계 또는 재료와 같이 수용 가능성의 한계를 설명하는 엔지니어링의 공차 구간과 구별합니다. 일반적으로 편의상 단순히 “허용 오차 구간”으로 설명합니다.

공차 구간은 두 수량으로 정의됩니다.

적용 범위: 구간이 적용되는 모집단의 비율입니다.
신뢰도: 구간이 모집단의 비율을 포함한다는 확률적 신뢰도입니다.

공차 구간은 커버리지와 공차 계수의 두 가지 계수를 사용하여 데이터로 구성됩니다. 적용 범위는 구간에 포함되어야 하는 모집단(p)의 비율입니다. 공차 계수는 구간이 지정된 범위에 도달하는 신뢰도입니다. 적용 범위가 95%이고 공차 계수가 90%인 공차 구간에는 신뢰 수준이 90%인 모집단 분포의 95%가 포함됩니다.

— 페이지 175, 환경 엔지니어를 위한 통계, 제2판, 2002.

공차 구간 계산 방법

공차 구간의 크기는 모집단의 데이터 표본 크기와 모집단의 분산에 비례합니다.

데이터 분포에 따라 공차 구간을 계산하는 두 가지 주요 방법은 모수 방법과 비모수 방법입니다.

모수 공차 구간: 적용 범위와 신뢰도를 모두 지정할 때 모집단 분포에 대한 지식을 사용합니다. 종종 가우스 분포를 나타내는 데 사용됩니다.
비모수 공차 구간: 순위 통계량을 사용하여 적용 범위와 신뢰도를 추정하면 분포에 대한 정보가 부족하여 정밀도(구간이 더 넓어짐)가 떨어지는 경우가 많습니다.

공차 구간은 가우스 분포에서 추출한 독립 관측치의 표본에 대해 계산하기가 비교적 간단합니다. 다음 섹션에서 이 계산을 보여 드리겠습니다.

가우스 분포에 대한 공차 구간

이 섹션에서는 데이터 샘플에 대한 공차 구간을 계산하는 예를 살펴보겠습니다.

먼저 데이터 샘플을 정의해 보겠습니다. 가우스 분포에서 추출한 100개의 관측치로 구성된 표본을 생성하며, 평균은 50이고 표준 편차는 5입니다.

1
2
# generate dataset
data = 5 * randn(100) + 50

이 예제에서는 실제 모집단 평균과 표준 편차를 알지 못하며 이러한 값을 추정해야 한다고 가정합니다.

모집단 모수를 추정해야 하기 때문에 추가적인 불확실성이 있습니다. 예를 들어, 95% 적용 범위의 경우 추정된 평균에서 1.96(또는 2) 표준 편차를 공차 구간으로 사용할 수 있습니다. 표본에서 평균과 표준 편차를 추정하고 이 불확실성을 고려해야 하므로 구간 계산이 약간 더 복잡합니다.

다음으로 자유도 수를 지정해야 합니다. 이것은 임계 값 계산 및 간격 계산에 사용됩니다. 구체적으로는 표준 편차의 계산에 사용됩니다.

자유도는 계산에서 달라질 수 있는 값의 수입니다. 여기에는 100 개의 관측치가 있으므로 100 자유도가 있습니다. 표준 편차를 모르기 때문에 평균을 사용하여 추정해야 합니다. 이것은 우리의 자유도가 (N – 1) 또는 99가 됨을 의미합니다.

1
2
3
# specify degrees of freedom
n = len(data)
dof = n – 1

다음으로 데이터의 비례 범위를 지정해야합니다. 이 예에서는 데이터의 중간 95%에 관심이 있습니다. 비율은 95입니다. 중간 95%, 즉 2.5번째 백분위수에서 97.5번째 백분위수로 이 비율을 이동해야 합니다.

우리는 95%의 임계값이 너무 자주 사용된다는 점을 감안할 때 1.96이라는 것을 알고 있습니다. 그럼에도 불구하고 역 생존 함수의 백분율 2.5%가 주어지면 Python에서 직접 계산할 수 있습니다. 이것은 norm.isf() SciPy 함수를 사용하여 계산할 수 있습니다.

1
2
3
4
# specify data coverage
prop = 0.95
prop_inv = (1.0 – prop) / 2.0
gauss_critical = norm.isf(prop_inv)

다음으로 적용 범위의 신뢰도를 계산해야 합니다. 주어진 자유도와 원하는 확률에 대한 카이 제곱 분포에서 임계값을 검색하여 이를 수행할 수 있습니다. chi2.isf() SciPy 함수를 사용할 수 있습니다.

1
2
3
# specify confidence
prob = 0.99
chi_critical = chi2.isf(q=prob, df=dof)

이제 가우스 공차 구간을 계산하는 모든 조각이 있습니다. 계산은 다음과 같습니다.

1
interval = sqrt((dof * (1 + (1/n)) * gauss_critical^2) / chi_critical)

여기서 dof는 자유도의 수이고, n은 데이터 표본의 크기이고 gauss_critical은 모집단의 95% 커버리지에 대한 1.96과 같은 임계값이고,chi_critical은 원하는 신뢰 수준과 자유도에 대한 카이 제곱 임계값입니다.

1
interval = sqrt((dof * (1 + (1/n)) * gauss_critical**2) / chi_critical)

이 모든 것을 함께 묶고 데이터 샘플에 대한 가우스 허용 오차 구간을 계산할 수 있습니다.

전체 예제는 다음과 같습니다.

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
# parametric tolerance interval
from numpy.random import seed
from numpy.random import randn
from numpy import mean
from numpy import sqrt
from scipy.stats import chi2
from scipy.stats import norm
# seed the random number generator
seed(1)
# generate dataset
data = 5 * randn(100) + 50
# specify degrees of freedom
n = len(data)
dof = n – 1
# specify data coverage
prop = 0.95
prop_inv = (1.0 – prop) / 2.0
gauss_critical = norm.isf(prop_inv)
print(‘Gaussian critical value: %.3f (coverage=%d%%)’ % (gauss_critical, prop*100))
# specify confidence
prob = 0.99
chi_critical = chi2.isf(q=prob, df=dof)
print(‘Chi-Squared critical value: %.3f (prob=%d%%, dof=%d)’ % (chi_critical, prob*100, dof))
# tolerance
interval = sqrt((dof * (1 + (1/n)) * gauss_critical**2) / chi_critical)
print(‘Tolerance Interval: %.3f’ % interval)
# summarize
data_mean = mean(data)
lower, upper = data_mean–interval, data_mean+interval
print(‘%.2f to %.2f covers %d%% of data with a confidence of %d%%’ % (lower, upper, prop*100, prob*100))

예제를 실행하면 먼저 가우스 분포와 카이 제곱 분포에 대한 관련 임계값이 계산되고 인쇄됩니다. 허용 오차가 인쇄 된 다음 올바르게 표시됩니다.

1
2
3
4
Gaussian critical value: 1.960 (coverage=95%)
Chi-Squared critical value: 69.230 (prob=99%, dof=99)
Tolerance Interval: 2.355
47.95 to 52.66 covers 95% of data with a confidence of 99%

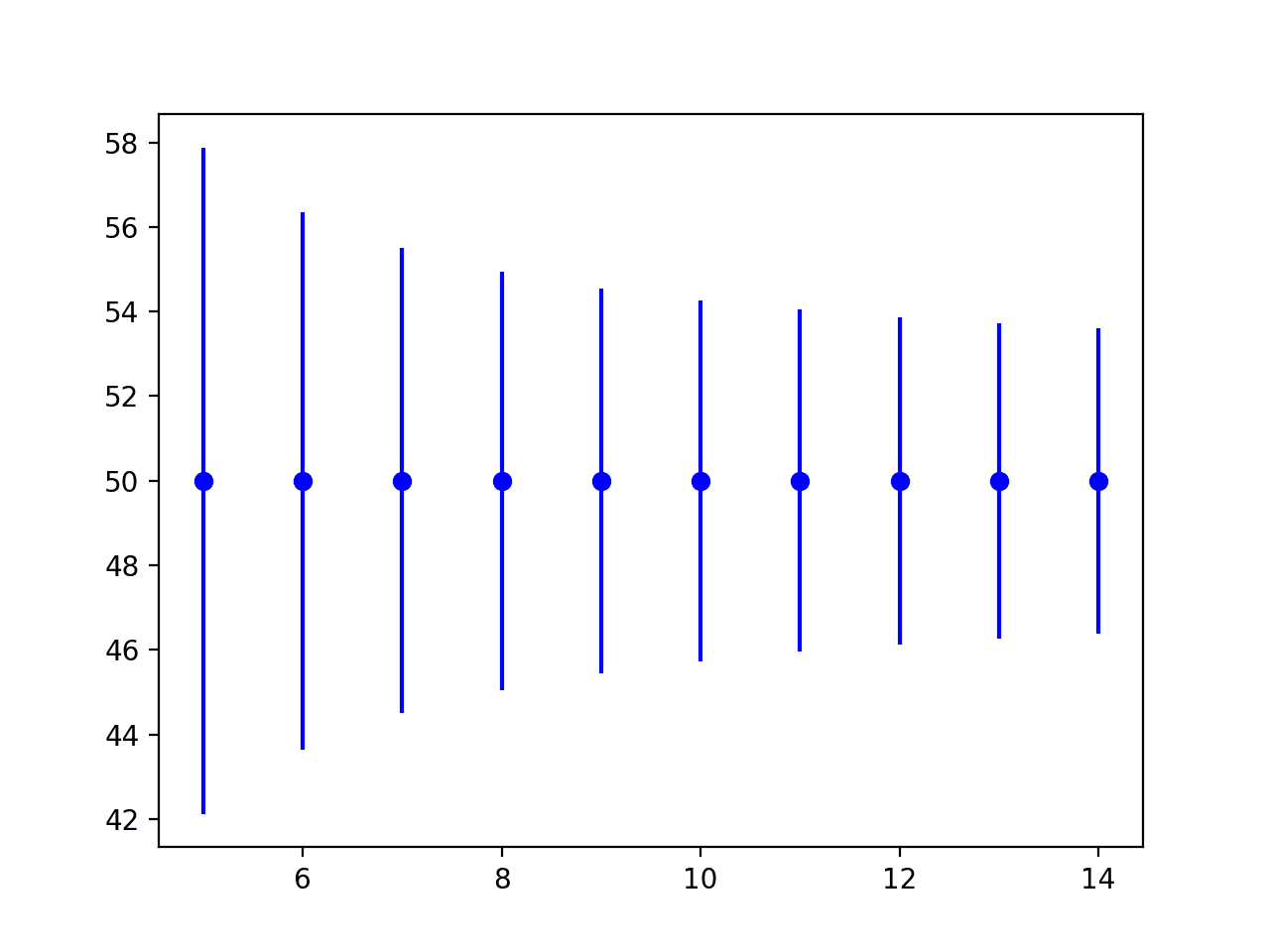
또한 표본의 크기가 증가함에 따라 공차 구간이 어떻게 감소하는지(더 정확해짐)를 보여주는 것도 도움이 될 수 있습니다.

아래 예제에서는 동일한 작은 인위적인 문제에 대해 서로 다른 표본 크기에 대한 공차 구간을 계산하여 이를 보여줍니다.

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
# plot tolerance interval vs sample size
from numpy.random import seed
from numpy.random import randn
from numpy import sqrt
from scipy.stats import chi2
from scipy.stats import norm
from matplotlib import pyplot
# seed the random number generator
seed(1)
# sample sizes
sizes = range(5,15)
for n in sizes:
    # generate dataset
    data = 5 * randn(n) + 50
    # calculate degrees of freedom
    dof = n – 1
    # specify data coverage
    prop = 0.95
    prop_inv = (1.0 – prop) / 2.0
    gauss_critical = norm.isf(prop_inv)
    # specify confidence
    prob = 0.99
    chi_critical = chi2.isf(q=prob, df=dof)
    # tolerance
    tol = sqrt((dof * (1 + (1/n)) * gauss_critical**2) / chi_critical)
    # plot
    pyplot.errorbar(n, 50, yerr=tol, color=’blue’, fmt=’o’)
    # plot results                                                                                                                         
    pyplot.show()

예제를 실행하면 실제 모집단 평균 주위의 공차 구간을 보여주는 그림이 생성됩니다.

표본 크기가 5개에서 15개 예제로 증가함에 따라 간격이 더 작아지는 것을 볼 수 있습니다(더 정확함).

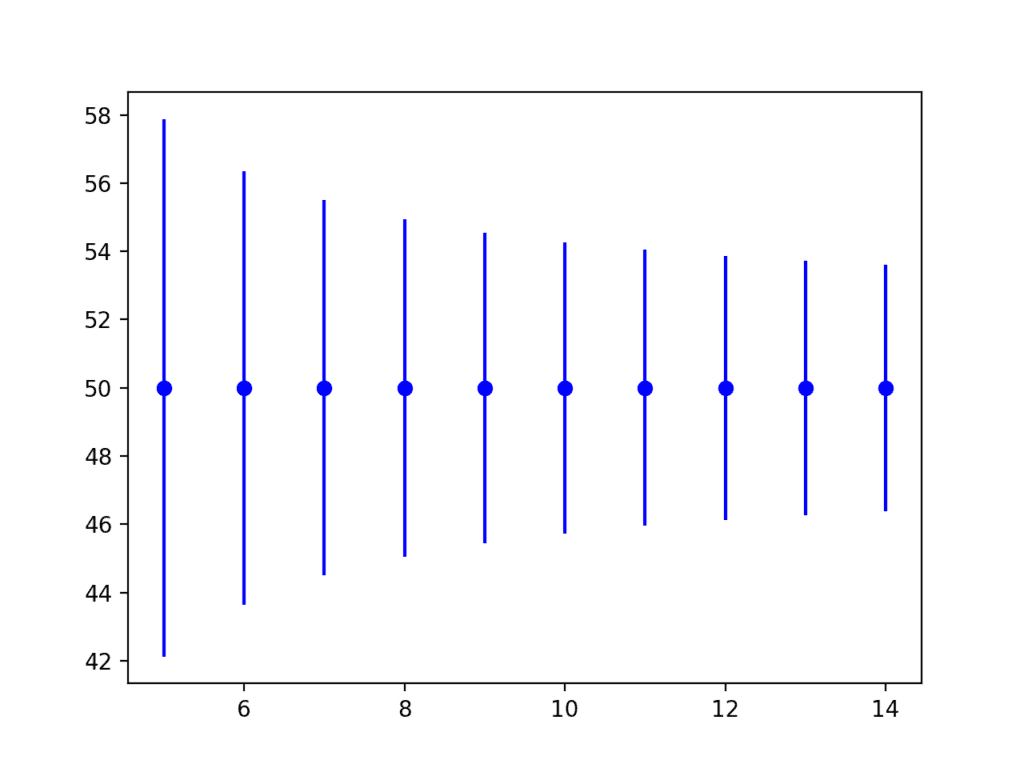
Error Bar Plot of Tolerance Interval vs Sample Size

공차 구간 대 표본 크기의 오차 막대 그림

확장

이 섹션에는 탐색할 수 있는 자습서를 확장하기 위한 몇 가지 아이디어가 나열되어 있습니다.

머신러닝 프로젝트에서 허용 오차 구간을 사용할 수 있는 3가지 사례를 나열합니다.
가우스 변수가 있는 데이터셋을 찾고 이에 대한 공차 구간을 계산합니다.
비모수 공차 구간을 계산하는 한 가지 방법을 조사하고 설명하십시오.

추가 정보

이 섹션에서는 더 자세히 알아보려는 경우 주제에 대한 더 많은 리소스를 제공합니다.

책

API

기사

요약

이 자습서에서는 통계적 공차 구간과 가우스 데이터에 대한 공차 구간을 계산하는 방법을 알아보았습니다.

특히 다음 내용을 배웠습니다.

이 통계적 공차 구간은 모집단의 관측치에 대한 한계를 제공합니다.
공차 구간을 사용하려면 커버리지 비율과 신뢰 수준을 모두 지정해야 합니다.
가우스 분포를 갖는 데이터 샘플에 대한 허용 오차 구간을 쉽게 계산할 수 있습니다.

Tags:

Machine learning,Statistical Tolerance Intervals