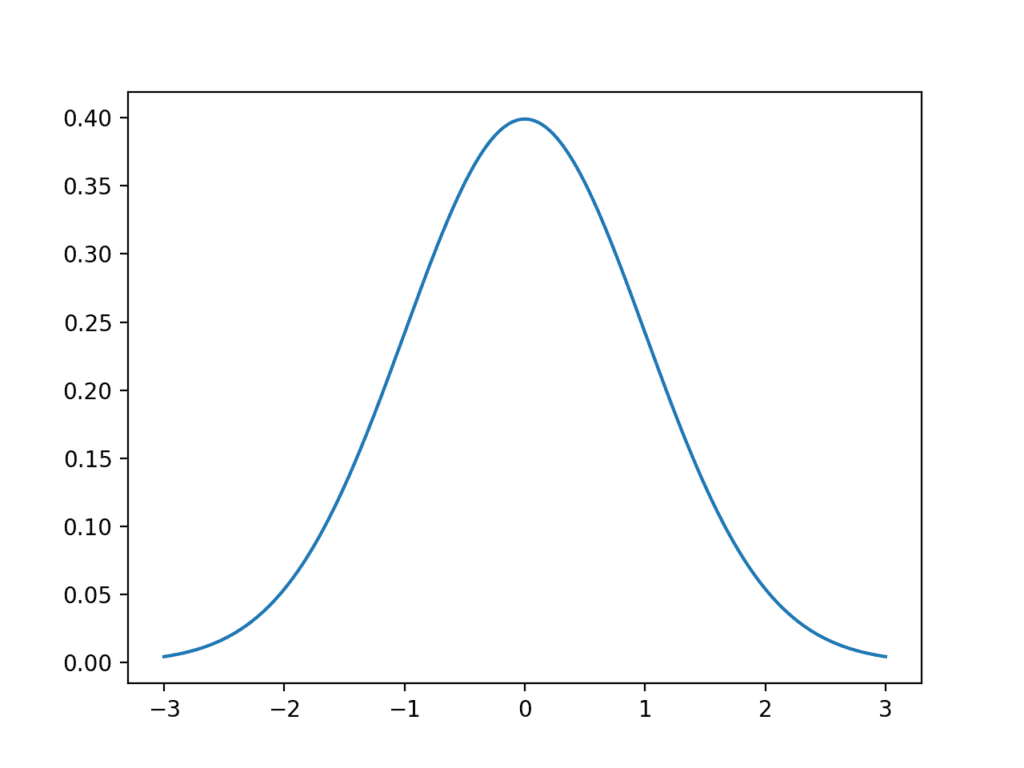
데이터 샘플은 도메인에서 생성되거나 프로세스에서 생성될 수 있는 모든 가능한 관측치의 광범위한 모집단의 스냅샷입니다. 흥미롭게도 많은 관측치는 정규 분포 또는 더 공식적으로 가우스 분포라고 하는 일반적인 패턴이나 분포에 적합합니다. 가우스 분포에 대해 많이 알려져 있으며, 따라서 가우스 데이터와 함께 사용할 수있는 통계 및 통계 방법의 전체 하위 필드가 있습니다. 이 자습서에서는 가우스 분포, 가우스 분포를 […]
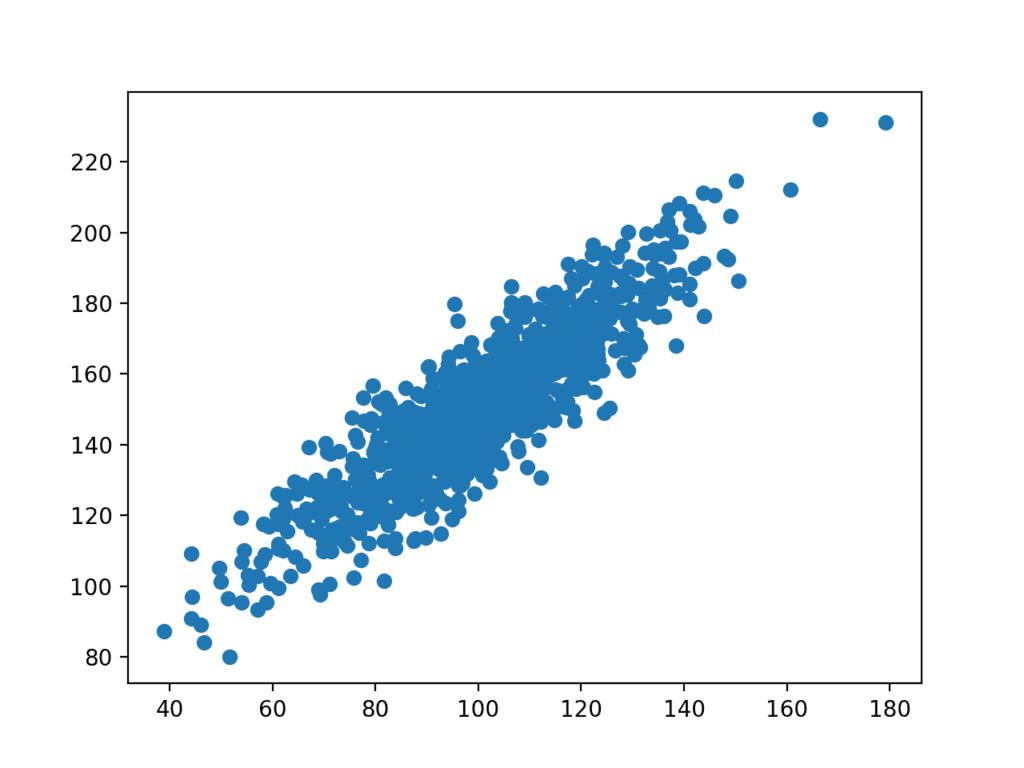
데이터 세트의 변수 간에 복잡하고 알 수 없는 관계가 있을 수 있습니다. 데이터 세트의 변수가 서로 의존하는 정도를 발견하고 정량화하는 것이 중요합니다. 이 지식은 선형 회귀와 같은 머신러닝 알고리즘의 기대치를 충족하도록 데이터를 더 잘 준비하는 데 도움이 될 수 있으며, 이러한 상호 종속성이 있을 경우 성능이 저하됩니다. 이 자습서에서는 상관 관계가 변수 간의 관계에 대한 통계적 요약이며 […]
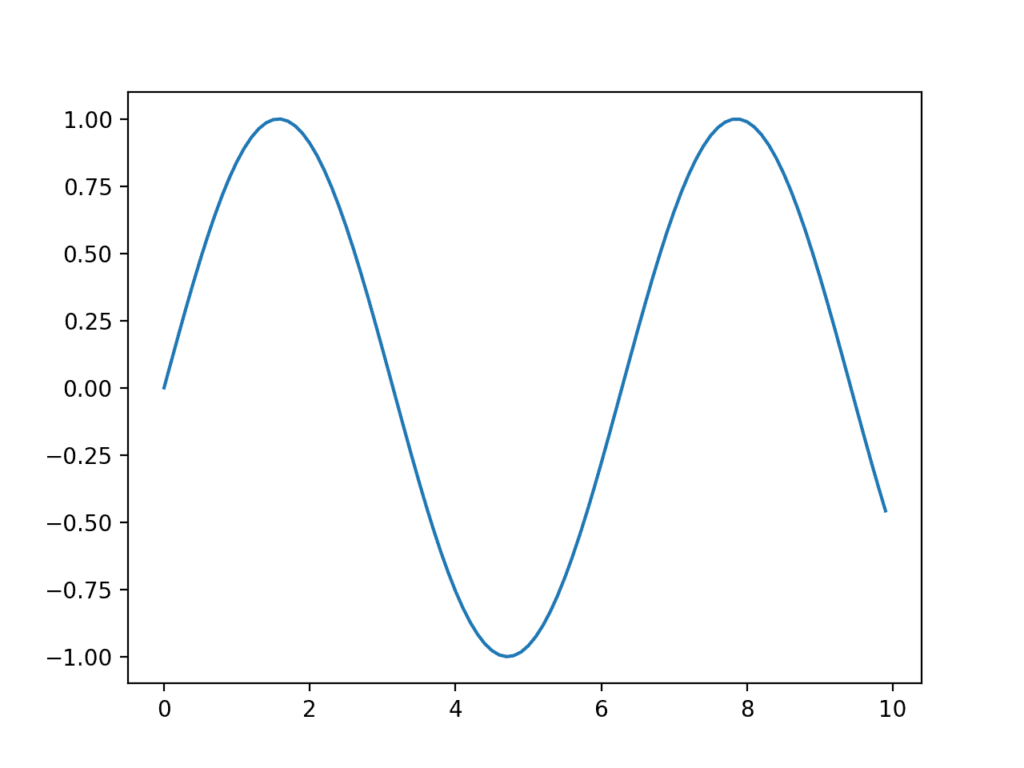
때로는 차트 및 플롯과 같은 시각적 형태로 볼 수 있을 때까지는 데이터가 의미가 없습니다. 자신과 다른 사람을 위해 데이터 샘플을 빠르게 시각화 할 수 있는 것은 응용 통계와 응용 머신러닝 모두에서 중요한 기술입니다. 이 튜토리얼에서는 Python에서 데이터를 시각화 할 때 알아야 할 5가지 유형의 플롯과 이를 사용하여 자신의 데이터를 더 잘 이해하는 방법을 알아봅니다. 이 […]
데이터 요약은 몇 가지 통계 값만으로 데이터 샘플의 모든 값을 설명하는 편리한 방법을 제공합니다. 평균과 표준 편차는 가우스 분포로 데이터를 요약하는 데 사용되지만, 데이터 표본에 비가우스 분포가 있는 경우 의미가 없거나 오해의 소지가 있을 수도 있습니다. 이 자습서에서는 특정 데이터 분포를 가정하지 않고 데이터 샘플의 분포를 설명하기 위한 5자리 숫자 요약을 발견합니다. 이 자습서를 완료하면 […]
통계는 머신러닝에 대한 더 깊은 이해를 위한 전제 조건으로 널리 받아들여지는 수학 분야입니다. 통계학은 많은 난해한 이론과 발견이 있는 큰 분야이지만, 머신러닝 실무자에게는 현장에서 가져온 너트와 볼트 도구와 표기법이 필요합니다. 통계가 무엇인지에 대한 견고한 기초가 있으면 좋은 부분이나 관련성 있는 부분에만 집중할 수 있습니다. 이 집중 코스에서는 7일 만에 머신러닝에 사용되는 통계 방법을 시작하고 자신 있게 […]
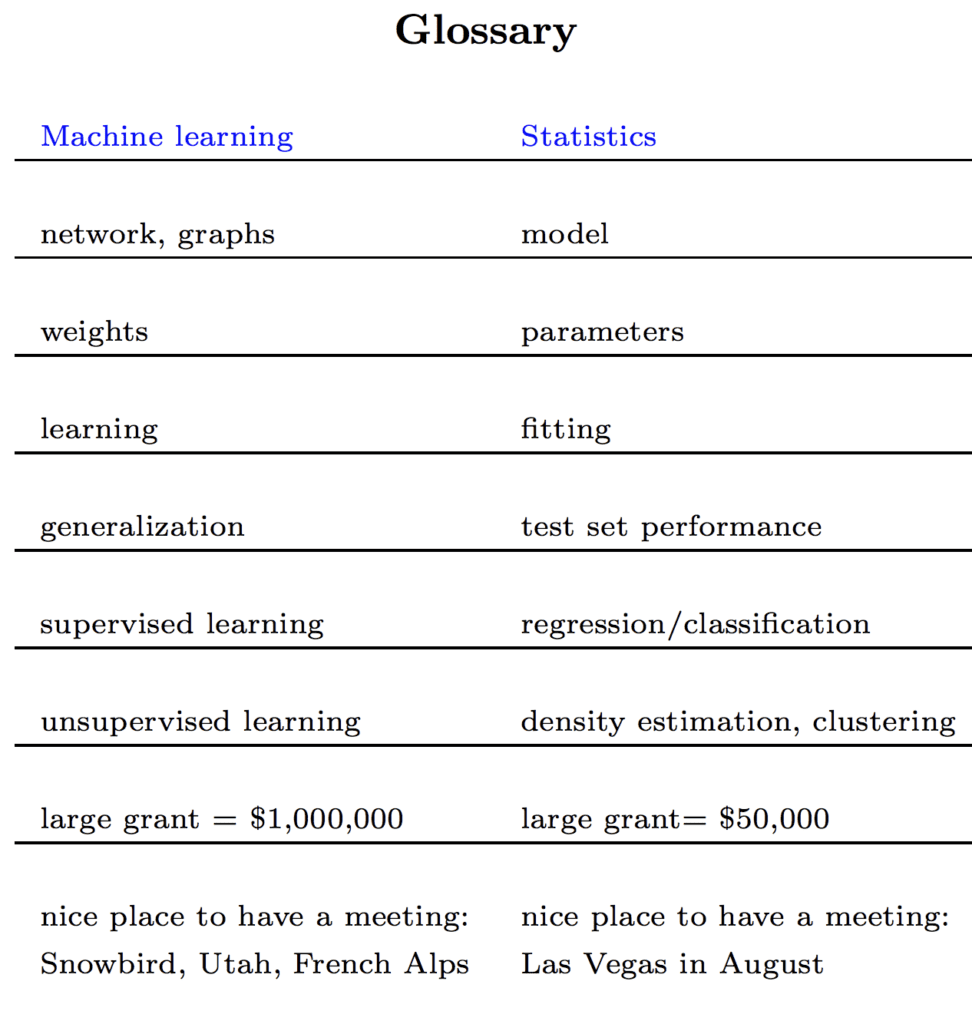
통계와 머신러닝은 매우 밀접하게 관련된 두 분야입니다. 사실, 둘 사이의 경계는 때때로 매우 흐릿할 수 있습니다. 그럼에도 불구하고 통계 분야에 분명히 속하는 방법이 있는데, 이는 유용할 뿐만 아니라 머신러닝 프로젝트를 수행할 때 매우 중요합니다. 머신러닝 예측 모델링 프로젝트를 효과적으로 수행하려면 통계적 방법이 필요하다고 말할 수 있습니다. 이 게시물에서는 예측 모델링 문제의 주요 단계에서 유용하고 필요한 통계적 방법의 […]
머신러닝 실무자는 알고리즘의 전통과 모델 해석 가능성과 같은 다른 관심사보다 결과 및 모델 기술에 실용적인 초점을 가지고 있습니다. 통계학자들은 응용 통계와 통계 학습이라는 이름으로 거의 동일한 유형의 모델링 문제를 연구합니다. 수학적 배경에서 온 그들은 모델의 동작과 예측의 설명 가능성에 더 중점을 둡니다. 동일한 문제에 대한 두 접근 방식 간의 매우 밀접한 관계는 두 분야가 서로에게서 […]
통계는 데이터에 대한 중요한 질문에 대한 답변을 얻기 위해 사용할 수 있는 도구 모음입니다. 기술 통계 방법을 사용하여 원시 관측치를 이해하고 공유할 수 있는 정보로 변환할 수 있습니다. 추론 통계 방법을 사용하여 작은 데이터 샘플에서 전체 도메인으로 추론할 수 있습니다. 이 게시물에서는 일반적으로 통계가 중요한 이유와 머신러닝 및 일반적으로 사용 가능한 방법 유형을 명확하게 발견하게 […]
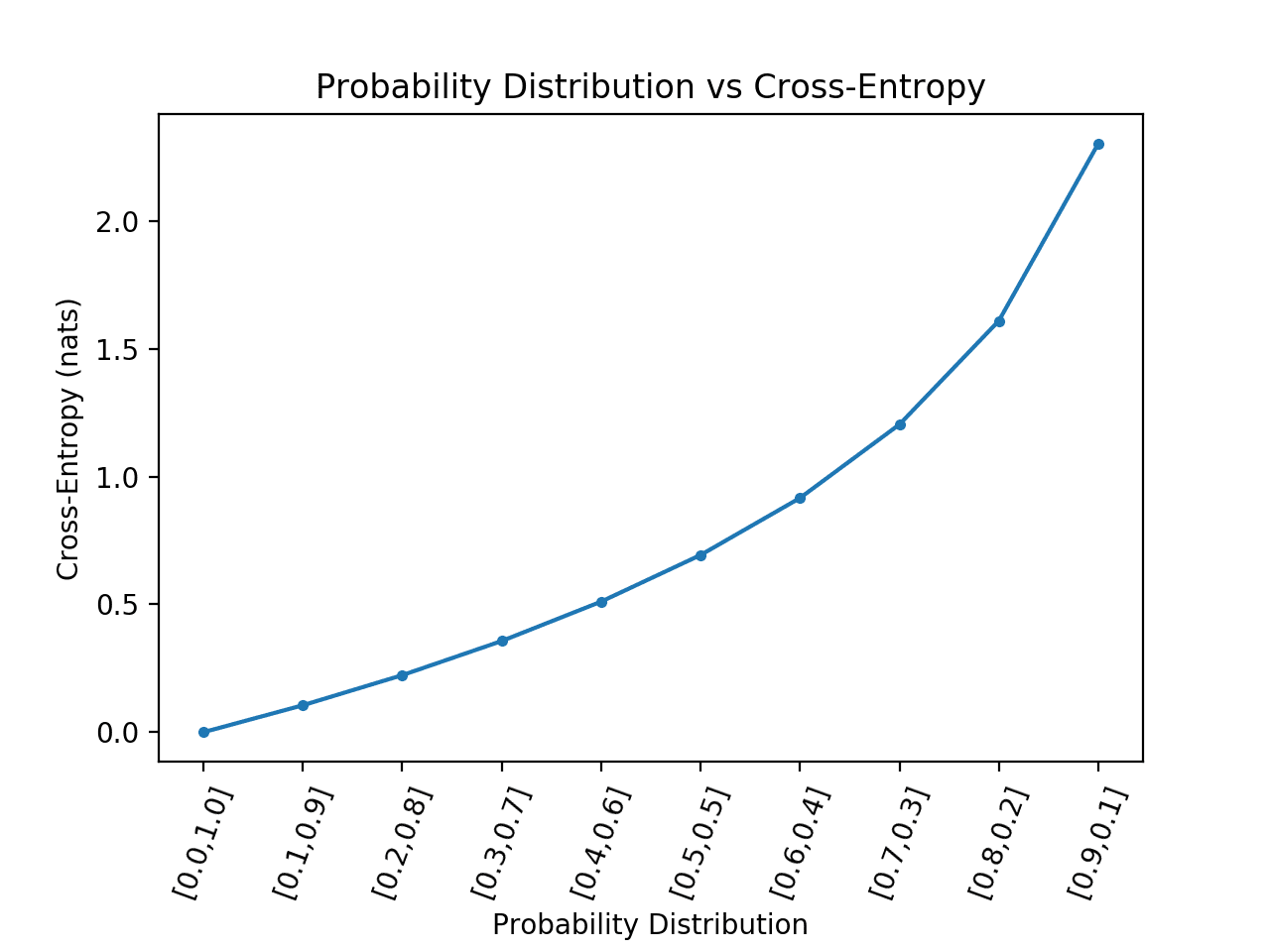
교차 엔트로피는 일반적으로 머신러닝에서 손실 함수로 사용됩니다. 교차 엔트로피는 엔트로피를 기반으로 하고 일반적으로 두 확률 분포의 차이를 계산하는 정보 이론 분야의 척도입니다. 두 확률 분포 사이의 상대 엔트로피를 계산하는 KL 발산과는 밀접한 관련이 있지만 다른 반면, 교차 엔트로피는 분포 사이의 총 엔트로피를 계산하는 것으로 생각할 수 있습니다. 교차 엔트로피는 또한 로지스틱 손실이라 불리는 로그 손실과 관련이 있으며 종종 […]
주어진 확률 변수에 대한 확률 분포 간의 차이를 정량화 하는 것이 종종 바람직합니다. 이것은 실제 확률 분포와 관찰 된 확률 분포의 차이를 계산하는 데 관심이 있을 수 있는 머신러닝에서 자주 발생합니다. 이것은 Kullback-Leibler Divergence (KL 발산) 또는 상대 엔트로피와 같은 정보 이론의 기술과 KL 발산의 정규화 되고 대칭적인 버전을 제공하는 Jensen-Shannon Divergence를 사용하여 달성 할 […]